-
Giải Toán 12 tập 1 - Cùng khám phá
-
Giải Toán 12 tập 2 - Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Bài 4. Khảo sát và vẽ đồ thị hàm số - Toán 12 Cùng khám..
Giải mục 2 trang 26 SGK Toán 12 tập 1 - Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: a) (y = f(x) = - {x^3} + 2{x^2} + 4x - 3) b) (y = f(x) = frac{1}{3}{x^3} - {x^2} + x + 1)
LT1
Trả lời câu hỏi Luyện tập 1 trang 26 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = f(x) = - {x^3} + 2{x^2} + 4x - 3\)
b) \(y = f(x) = \frac{1}{3}{x^3} - {x^2} + x + 1\)
Phương pháp giải:
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
Lời giải chi tiết:
a)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 2{x^2} + 4x - 3} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 - \frac{2}{x} - \frac{4}{{{x^2}}} + \frac{3}{{{x^3}}}} \right)} \right] = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 2{x^2} + 4x - 3} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 - \frac{2}{x} - \frac{4}{{{x^2}}} + \frac{3}{{{x^3}}}} \right)} \right] = + \infty \)
\({y^\prime } = 0 \leftrightarrow - 3{x^2} + 4x + 4 = 0 \leftrightarrow x = 2{\rm{ }}\)hoặc \(x = - \frac{2}{3}\)
Bảng biến thiên:
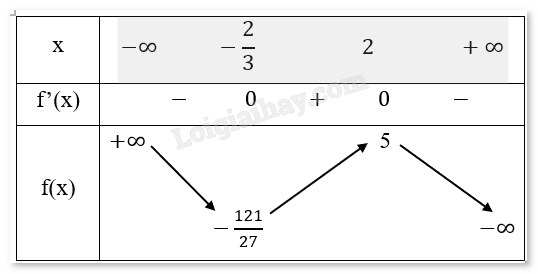
Chiều biến thiên: Hàm số nghịch biến trên các khoảng \(( - \infty - \frac{2}{3})\) và \((2; + \infty )\), đồng biến trên khoảng \(( - \frac{2}{3};2)\).
Cực trị: Hàm số đạt cực tiểu tại \(x = - \frac{2}{3},{y_{CT}} = - \frac{{121}}{{27}}.\)
Hàm số đạt cực đại tại \(x = 2,{y_{CD}} = 5.\)
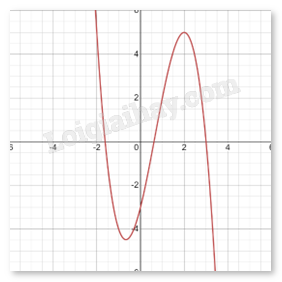
- Vẽ đồ thị:
Giao điểm với trục Oy là \((0, - 3)\).
Giao điểm với trục Ox là \((3,0)\left( {\frac{{ - 1 + \sqrt 5 }}{2},0} \right),\left( {\frac{{ - 1 - \sqrt 5 }}{2},0} \right)\).
b)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{1}{3}{x^3} - {x^2} + x + 1} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^3}\left( {\frac{1}{3} - \frac{1}{x} + \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right] = + \infty .\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{1}{3}{x^3} - {x^2} + x + 1} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( {\frac{1}{3} - \frac{1}{x} + \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right] = - \infty .\)
Ta có:
\({y^\prime } = {x^2} - 2x + 1\)
\({y^\prime } = 0 \leftrightarrow {x^2} - 2x + 1 = 0 \leftrightarrow x = 1\)
Bảng biến thiên:
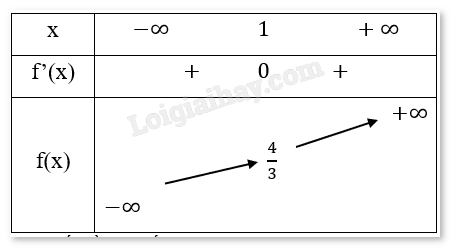
Chiều biến thiên: Hàm số đồng biến trên R
Cực trị: Vì hàm số đồng biến trên R nên hàm số không có điểm cực trị
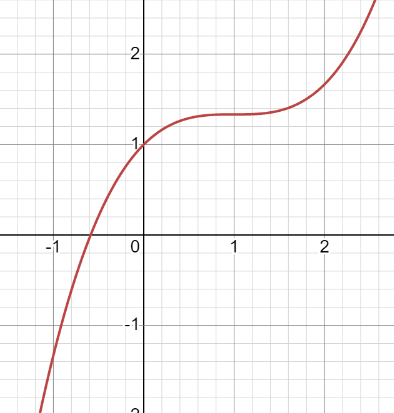
- Vẽ đồ thị:
Giao điểm với trục Oy là (0,1).
Giao điểm với trục Ox là (−0.5874,0).
VD1
Trả lời câu hỏi Vận dụng 1 trang 26 SGK Toán 12 Cùng khám phá
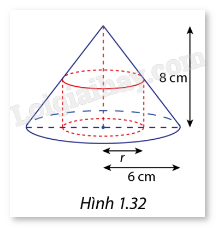
Một chi tiết máy có dạng khối nón với bán kính đáy là 6 cm và chiều cao là 8 cm. Người ta cần khoan từ đáy khối nón lên phía trên một khối trụ có bán kính đáy là r (r > 0)và có tâm của đáy trùng tâm của đáy khối nón như Hình 1.32. Xác định r sao cho phần thể tích khối trụ có được là lớn nhất.
Phương pháp giải:
- Biểu diễn thể tích khối trụ cần khoan trong khối nón
- Biểu diễn chiều cao h của khối trụ theo bán kính r
- Xác giá trị r để thể tích khối trụ V lớn nhất bằng cách tìm giá trị lớn nhất của V trong khoảng (0, \( + \infty )\).
Lời giải chi tiết:
Ta có thể tích khối trụ là:
\(V = \pi {r^2}h\)
Sử dụng tỷ lệ hình học trong tam giác đồng dạng:
\(\frac{h}{8} = \frac{{6 - r}}{6} \to h = 8.\frac{{6 - r}}{6} = 8 - \frac{{8r}}{6} = 8 - \frac{{4r}}{3}\)
Thay h vào công thức tính thể tích V:
\(V = \pi {r^2}\left( {8 - \frac{{4r}}{3}} \right) = \pi {r^2} \cdot \frac{{24 - 4r}}{3} = \pi \cdot \frac{{24{r^2} - 4{r^3}}}{3} = \frac{\pi }{3}\left( {24{r^2} - 4{r^3}} \right)\)
Đạo hàm V theo r:
\(\frac{{dV}}{{dr}} = \frac{\pi }{3}\left( {48r - 12{r^2}} \right) = \frac{\pi }{3} \cdot 12r(4 - r) = 4\pi r(4 - r)\)
Với \(\frac{{dV}}{{dr}} = 0\) thì ta có 2 nghiệm r là \(r = 0\) hoặc \(r = 4\) (Loại \(r = 0\) vì \(r > 0\))
Lập bảng biến thiên của hàm số \(f(x) = \frac{\pi }{3}\left( {24{x^2} - 4{x^3}} \right)\)
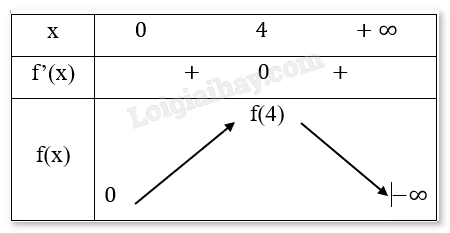
Nhận thấy khi x = 0 thì giá trị của f(x) là lớn nhất
Vậy giá trị bán kính r sao cho phần thể tích khối trụ có được là lớn nhất là r = 4cm.
Bình luận
Chia sẻ
- Giải mục 3 trang 28 SGK Toán 12 tập 1 - Cùng khám phá
- Giải mục 4 trang 30 SGK Toán 12 tập 1 - Cùng khám phá
- Giải mục 5 trang 33, 34 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.20 trang 34 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.21 trang 34 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
