Giải chuyên đề học tập Toán lớp 10 Chân trời sáng tạo

Bài 2. Ứng dụng của hệ phương trình bậc nhất ba ẩn Chuy..

Giải mục 2 trang 15, 16, 17 Chuyên đề học tập Toán 10 - Chân trời sáng tạo

Một nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm,

Lựa chọn câu để xem lời giải nhanh hơn

Thực hành 2

Một nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm, để tạo ra 100ml dung dịch nồng độ 18%, nhà hóa học đã sử dụng lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40%. Tính số mililit dung dịch mỗi loại mà nhà hóa học đó đã sử dụng trong thí nghiệm này.

Phương pháp giải:

Bước 1: Lập hệ phương trình

+ Chọn ẩn và đặt điều kiện cho ẩn

+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết

+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng

Bước 2: Giải hệ phương trình

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết:

Gọi số mililit dung dịch mỗi loại 10%, 20% và 40% sử dụng trong thí nghiệm là x, y, z (đơn vị mililit) \((x,y,z > 0)\)

Tạo ra 100ml dung dịch mới nên ta có: \(x + y + z = 100\)

Khối lượng chất tan trong dung dịch mới là: \(10\% x + 20\% y + 40\% z = 18\% .100 \Leftrightarrow 0,1x + 0,2y + 0,4z = 18\)

Lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40% nên \(x = 4z\)

Từ đó ta có hệ phương trình bậc nhất ba ẩn:

\(\left\{ \begin{array}{l}x + y + z = 100\\0,1x + 0,2y + 0,4z = 18\\x - 4z = 0\end{array} \right.\)

Sử dụng máy tính cầm tay, ta được \(x = 40;y = 50;z = 10\)

Vậy nhà hóa học đó đã dùng 40ml dung dịch 10%, 50ml dung dịch 20%,10ml dung dịch 40%.

Vận dụng 1

Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3, 4, 7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra. Tính số tế bào con mỗi loại lúc ban đầu.

Phương pháp giải:

Bước 1: Lập hệ phương trình

+ Chọn ẩn và đặt điều kiện cho ẩn

+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết

+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng

Bước 2: Giải hệ phương trình

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết:

Gọi số tế bào con mỗi loại A, B, C lúc đầu là x, y, z (tế bào) \((x,y,z \in \mathbb{N})\)

Tổng số tế bào con tạo ra là 480 tế bào nên \(x{.2^3} + y{.2^4} + z{.2^7} = 480\)

Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C nên \(y = x + z\)

Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra nên \(x{.2^3} + z{.2^7} = 5y{.2^4}\)

Từ đó ta có hệ phương trình bậc nhất ba ẩn:

\(\left\{ \begin{array}{l}x{.2^3} + y{.2^4} + z{.2^7} = 480\\y = x + z\\x{.2^3} + z{.2^7} = 5y{.2^4}\end{array} \right.\)

Sử dụng máy tính cầm tay, ta được \(x = 2;y = 5;z = 3\)

Vậy ban đầu có 2 tế bào loại A, 5 tế bào loại B và 3 tế bào loại C.

Vận dụng 2

Cho sơ đồ mạch điện như Hình 2. Tính các cường độ dòng điện \({I_1},{I_2},{I_3}\)

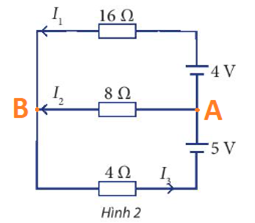
Phương pháp giải:

Bước 1: Lập hệ phương trình

+ Chọn ẩn và đặt điều kiện cho ẩn

+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết

+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng

Bước 2: Giải hệ phương trình

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết:

Ta có:

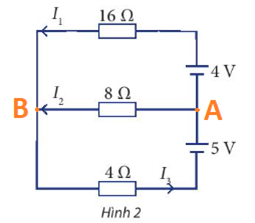
\(\left. \begin{array}{l}{U_{AB}} = - {E_1} + {I_1}{R_1} = - 4 + 16{I_1}\\{U_{AB}} = {I_2}{R_2} = 8{I_2}\\{U_{AB}} = {E_2} - {I_3}{R_3} = 5 - 4{I_3}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l} - 4 + 16{I_1} = 8{I_2}\\5 - 4{I_3} = 8{I_2}\end{array} \right.\)

Tại nút B: \({I_1} + {I_2} = {I_3}\)

Từ đó ta có hệ phương trình bậc nhất ba ẩn:

\(\left\{ \begin{array}{l}16{I_1} - 8{I_2} = 4\\8{I_2} + 4{I_3} = 5\\{I_1} + {I_2} - {I_3} = 0\end{array} \right.\)

Sử dụng máy tính cầm tay, ta được \({I_1} = \frac{{11}}{{28}},{I_2} = \frac{2}{7},{I_3} = \frac{{19}}{{28}}\)

Vậy \({I_1} = \frac{{11}}{{28}}A,{I_2} = \frac{2}{7}A,{I_3} = \frac{{19}}{{28}}A\)

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 6 phiếu

Bài tiếp theo

Giải mục 3 trang 20 Chuyên đề học tập Toán 10 - Chân trời sáng tạo
Xét thị trường chè, cà phê và cacao. Gọi x,y và z lần lượt là giá của 1kg chè, 1 kg cà phê và 1 kg ca cao (đơn vị: nghìn đồng, \(x \ge 0,y \ge 0,z \ge 0\)). Các lượng cung và lượng cầu của mỗi sản phẩm được cho như bảng sau
Giải bài 1 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Một đại lí bán ba mẫu máy điều hoà A, B và C, với giá bán mỗi chiếc theo từng mẫu làn lượt là 8 triệu đồng, 10 triệu đồng và 12 triệu đồng.
Giải bài 2 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Nhân dịp kỉ niệm ngày thành lập Đoàn Thanh niên Cộng sản Hồ Chí Minh, một trường Trung học phố thông đã tổ chức cho học sinh tham gia các trò chơi
Giải bài 3 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Một cửa hàng giải khát chỉ phục vụ ba loại sinh tố: xoài, bơ và mãng cầu. Để pha mỗi li (cốc) sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bang sau.
Giải bài 4 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Ba tế bào A, B, C sau một số lần nguyên phân tạo ra 168 tế bào con. Biết số tế bào A tạo ra gấp bốn lần số tế bào B tạo ra và số lần nguyên phân của tế bào C nhiều hơn số lần nguyên phân của tế bào B là bốn lần. Tinh số lần nguyên phân của mỗi tế bào.
Giải bài 5 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Cho sơ đồ mạch điện như Hình 3. Biết \({R_1} = 4\Omega ,{\rm{ }}{R_2} = 4\Omega \) và \({R_3} = 8\Omega \). Tìm các cường độ dòng điện \({I_1},{I_2},{I_3}\).
Giải bài 6 trang 22 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Cân bằng phương trình phản ứng khi đốt cháy khí methane trong oxygen:
Giải bài 7 trang 22 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Một nhà máy có ba bộ phận cắt, may, đóng gói để sản phẩm ba loại sản phẩm: áo thun, áo sơ mi, áo khoác. Thời gian (tính bằng phút) của mỗi bộ phận để sản xuất 10 cái áo mỗi loại được thể hiện trong bảng sau:
Giải bài 8 trang 22 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Bà Hà có 1 tỉ đồng để đầu tư vào cổ phiếu, trái phiếu và gửi tiết kiệm ngân hàng.
Giải bài 9 trang 22 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Trên thị trường có ba loại sản phẩm A, B, C với ía mỗi tấn sản phẩm tương ứng là x, y, z (đơn vị: triệu đồng, \(x \ge 0,y \ge 0,z \ge 0\)).
Giải bài 10 trang 23 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Vé vào xem một vở kịch có ba mức giá khác nhau tùy theo khu vực ngồi trong nhà hát. Số lượng vé bán ra và doanh thu của ba suất diễn cho bởi bảng sau:
Giải mục 1 trang 14, 15, 16, 17 Chuyên đề học tập Toán 10 - Chân trời sáng tạo
Ba vận động viên Hùng, Dũng và Mạnh tham gia thi đấu nội dung ba môn phối hợp: chạy, bơi và đạp xe, trong đó tốc độ trung bình của họ trên mỗi chặng đua được cho ở bảng dưới đây.