Toán 8, giải toán lớp 8 chân trời sáng tạo Bài 4. Hệ số góc của đường thẳng Toán 8 chân trời sáng ..

Giải mục 1 trang 23, 24 SGK Toán 8 tập 2 – Chân trời sáng tạo


a) Trong mặt phẳng tọa độ (Oxy), cho đường thẳng

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Video hướng dẫn giải

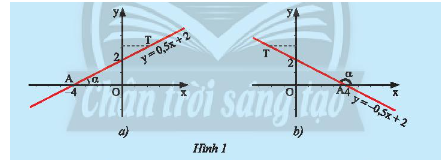
a) Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) cắt \(Ox\) tại điểm \(A\)  và \(T\) là một điểm trên đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có tung độ dương (Hình 1).

Ta gọi \(\alpha  = \widehat {xAT}\) là góc tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\).

Hãy nêu nhận xét của em về số đo của góc \(\alpha \) và hệ số \(a\) trong hai trường hợp dưới đây.

 

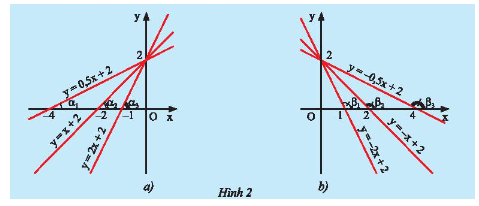
b) Hãy so sánh các hệ số \(a\) của các đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) trong mỗi hình ở Hình 2 và so sánh các góc \(\alpha \) hoặc các góc \(\beta \) tạo bởi các đường thẳng đó với trục \(Ox\).

Phương pháp giải:

- Góc vuông là góc có số đo bằng \(90^\circ \).

- Góc nhọn là góc có số đo nhỏ hơn \(90^\circ \).

- Góc tù là góc có số đo lớn hơn \(90^\circ \).

- Góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó.

Lời giải chi tiết:

a)

- Ở hình 1a là đồ thị của hàm số \(y = 0,5x + 2\) hệ số \(a = 0,5 > 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc nhọn.

- Ở hình 1b là đồ thị của hàm số \(y =  - 0,5x + 2\) hệ số \(a =  - 0,5 < 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc tù.

b)

- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).

Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).

Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).

- Ở hình 2b là đồ thị của 3 hàm số \(y =  - 2x + 2;y =  - x + 2;y =  - 0,5x + 2\).

Ta có: \({a_1} =  - 2;{a_2} =  - 1;{a_3} =  - 0,5\) nên \({a_1} < {a_2} < {a_3}\).

Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).

Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).

TH1

Video hướng dẫn giải

Tìm hệ số góc của các đường thẳng sau đây:

a) \(y =  - 5x - 5\);         

b) \(y = \sqrt 3 x + 3\);            

c) \(y = \sqrt {11} x + \sqrt 7 \)

Phương pháp giải:

Hệ số \(a\) là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).

Lời giải chi tiết:

a) Đường thẳng \(y =  - 5x - 5\) có hệ số góc là \(a =  - 5\).

b) Đường thẳng \(y = \sqrt 3 x + 3\) có hệ số góc là \(a = \sqrt 3 \).

c) Đường thẳng \(y = \sqrt {11} x + \sqrt 7 \) có hệ số góc là \(a = \sqrt {11} \).

VD1

Video hướng dẫn giải

Trong các đường thẳng sau, đường thẳng nào tạo với \(Ox\) một góc nhọn, đường thẳng nào tạo với \(Ox\) một góc tù?

a) \(y = 3x + 6\);            

b) \(y =  - 4x + 1\);         

c) \(y =  - 3x - 6\)

Phương pháp giải:

- Khi hệ số \(a\) dương \(\left( {a > 0} \right)\) thì góc \(\alpha \) tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\) là góc nhọn.

- Khi hệ số \(a\) âm \(\left( {a < 0} \right)\) thì góc \(\alpha \) tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\) là góc tù.

Lời giải chi tiết:

a) Đường thẳng \(y = 3x + 6\) có hệ số góc là \(a = 3 > 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là góc nhọn.

b) Đường thẳng \(y =  - 4x + 1\) có hệ số góc là \(a =  - 4 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.

c) Đường thẳng \(y =  - 3x - 6\) có hệ số góc là \(a =  - 3 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store