-
GIẢI SGK TOÁN 10 KẾT NỐI TRI THỨC VỚI CUỘC SỐNG - MỚI NHẤT
-
Toán 10 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 10 tập 2 - Kết nối tri thức với cuộc sống
Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống
Bài 16. Hàm số bậc hai Toán 10 Kết nối tri thức
Giải mục 1 trang 11, 12 SGK Toán 10 tập 2 - Kết nối tri thức
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức:
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
HĐ1
Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét \((0 < x < 10)\) là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x:
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.
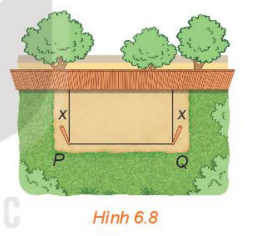
Lời giải chi tiết:
a) Theo bài ra ta có:
\(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\) (m).
b) Diện tích của mảnh đất được rào chắn là:
\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x\) \(({m^2})\).
CH
Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^4} + 3{x^2} + 2\);
B.\(y = \frac{1}{{{x^2}}}\);
C.\(y = - 3{x^2} + 1\);
D.\(y = 3{\left( {\frac{1}{x}} \right)^2} + 3.\frac{1}{x} - 1\).
Phương pháp giải:
Hàm số bậc hai là hàm số có dạng: \(y = a{x^2} + bx + c\) \((a \ne 0)\).
Lời giải chi tiết:
Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai.
LT1
Cho hàm số \(y = (x - 1)(2 - 3x)\).
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.
Phương pháp giải:
Hàm số có dạng \(a{x^2} + bx + c(a \ne 0)\) là hàm số bậc hai.
Lời giải chi tiết:
a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x \)
\(= - 3{x^2} + 5x - 2\).
Do đó hàm \(y=(x-1)(2-3x)\) là hàm số bậc hai với \(a = - 3\); \(b = 5\); \(c = - 2\).
b) Thay các giá trị của x vào \(y=(x-1)(2-3x)\) ta có:
VD1
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2}\); \(h\), \(t \ge 0\).
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
Lời giải chi tiết:
a) Để viên bi chạm đất thì \(h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\)
\(\Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\).
Do \(t \ge 0\) nên t = 2 (s).
Vậy sau 2 giây thì viên bi chạm đất.
b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\).
Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\).
\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\).
Bình luận
Chia sẻ
- Giải mục 2 trang 12, 13, 14, 15 SGK Toán 10 tập 2 - Kết nối tri thức
- Giải bài 6.7 trang 16 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.8 trang 16 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.9 trang 16 SGK Toán 10 – Kết nối tri thức
- Giải bài 6.10 trang 16 SGK Toán 10 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
Các bài khác cùng chuyên mục
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
- Lý thuyết Thực hành tính xác suất theo định nghĩa cổ điển - SGK Toán 10 Kết nối tri thức
- Lý thuyết Biến cố và định nghĩa cổ điển của xác suất - SGK Toán 10 Kết nối tri thức
- Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
- Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - SGK Toán 10 Kết nối tri thức
- Lý thuyết Quy tắc đếm - SGK Toán 10 Kết nối tri thức
