Giải bài tập 5 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo

Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Đọc kĩ dữ liệu để vẽ hình.

- Chứng minh tam giác MIO và tam giác MAO cùng nội tiếp một đường tròn thì tứ giác AMIO là một tứ giác nội tiếp.

Lời giải chi tiết

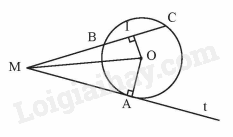
Xét tam giác OBC có OB = OC nên tam giác OBC cân tại O.

Mà I là trung điểm của BC nên BI là đường trung tuyến đồng thời là đường cao của tam giác OBC, suy ra \(OI \bot BC\) hay \(\widehat {OIM} = 90^\circ\).

Vì MA là tiếp tuyến của (O) nên \(MA \bot OA\) hay \(\widehat {OAM} = 90^\circ\).

Tam giác OIM và tam giác OAM vuông tại I và A nên hai tam giác này cùng nội tiếp đường tròn đường kính MO, do đó tứ giác AMIO là tứ giác nội tiếp đường tròn đường kính OM.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 6 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng: a) Tứ giác ABCD nội tiếp; b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.
Giải bài tập 7 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N. a) Chứng minh hai tam giác ABM và ADN bằng nhau. b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp. c) Chứng minh ba điểm B, D, O thẳng hàng.
Giải bài tập 4 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho hình vuông MNPQ nội tiếp đường tròn bán kính R. Tính độ dài cạnh và đường chéo của hình vuông theo R.
Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD trong mỗi trường hợp sau: a) AB = 6 cm, BC = 8 cm; b) AC = 9cm.
Giải bài tập 2 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác nhọn ABC. Gọi A’, B’, C’ lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp trong hình.
Giải bài tập 1 trang 73 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho ABCD là tứ giác nội tiếp. Hãy hoàn thành bảng sau vào vở.
Giải mục 3 trang 72 SGK Toán 9 tập 2 - Chân trời sáng tạo
a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD. b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Giải mục 2 trang 71 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4). a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp (widehat {DAB}) và (widehat {DCB}) b) Tính tổng số đo của các cung vừa tìm được. c) Nêu kết luận về tổng số đo của hai góc (widehat {DAB}) và (widehat {DCB}). d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
Giải mục 1 trang 70, 71 SGK Toán 9 tập 2 - Chân trời sáng tạo
Các tứ giác trong Hình 1 có đặc điểm gì giống nhau?
Lý thuyết Tứ giác nội tiếp Toán 9 Chân trời sáng tạo
1. Đường tròn ngoại tiếp của một tứ giác Định nghĩa đường tròn ngoại tiếp tứ giác - Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp). - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó.