Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá Ôn tập chương 4 - Toán 9 Cùng khám phá

Giải bài tập 4.19 trang 89 SGK Toán 9 tập 1 - Cùng khám phá


Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho. Khi tia sáng được truyền qua mặt phân cách giữa không khí và nước thì đường đi tia sáng sẽ bị lệch đi do hiện tượng khúc xạ ánh sáng. Góc tới i và góc khúc xạ r như Hình 4.33 liên hệ với nhau theo công thức \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\). Một con cá bơi ở vị trí C. Do ánh sáng bị khúc xạ nên Minh đứng trên bờ nhìn xuống nước với góc \(r = {54^o}\) thì thấy con cá ở vị trí A thẳng hàng với O, M v

Đề bài

Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.

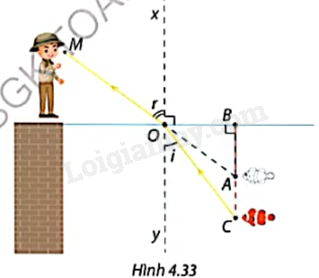
Khi tia sáng được truyền qua mặt phân cách giữa không khí và nước thì đường đi tia sáng sẽ bị lệch đi do hiện tượng khúc xạ ánh sáng. Góc tới i và góc khúc xạ r như Hình 4.33 liên hệ với nhau theo công thức \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\). Một con cá bơi ở vị trí C. Do ánh sáng bị khúc xạ nên Minh đứng trên bờ nhìn xuống nước với góc \(r = {54^o}\) thì thấy con cá ở vị trí A thẳng hàng với O, M và cách mặt nước một đoạn \(AB = 71cm\).

a) Tính góc tới i.

b) Tính độ sâu BC từ mặt nước đến vị trí thực sự mà con cá đang bơi.

Phương pháp giải - Xem chi tiết

a) Ta có: \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\) nên \(\sin i = \frac{3}{4}\sin r\), do đó tính được góc tới i.

b) Ta có: \(\widehat {yOA} = \hat r = {54^o}\), \(\widehat {AOB} = {90^o} - \widehat {yOA} = {36^o}\), \(\widehat {BOC} = {90^o} - \hat i\).

Tam giác AOB vuông tại B nên \(OB = AB.\cot \widehat {AOB}\).

Tam giác CBO vuông tại B nên \(BC = OB.\tan \widehat {BOC}\).

Lời giải chi tiết

a) Ta có: \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\) nên \(\sin i = \frac{3}{4}\sin r = \frac{3}{4}\sin {54^o} \approx 0,6\), do đó, \(\widehat i \approx {37^o}21'\).

b) Ta có: \(\widehat {yOA} = \hat r = {54^o}\), \(\widehat {AOB} = {90^o} - \widehat {yOA} = {36^o}\), \(\widehat {BOC} = {90^o} - \hat i \approx {52^o}39'\)

Tam giác AOB vuông tại B nên

\(OB = AB.\cot \widehat {AOB} = 71.\cot {36^o} \approx 97,7\left( {cm} \right)\)

Tam giác CBO vuông tại B nên

\(BC = OB.\tan \widehat {BOC} \approx 97,7.\tan {52^o}39' \approx 128\left( {cm} \right)\)

Vậy độ sâu từ mặt nước đến vị trí thực sự mà con cá đang bơi là khoảng 128cm.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải bài tập 4.20 trang 89 SGK Toán 9 tập 1 - Cùng khám phá

    Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho. Người ta làm một con đường gồm ba đoạn AB, BC, CD bao quanh hồ nước như Hình 4.34. Tính khoảng cách AD. Gợi ý: Từ điểm A, kẻ đường vuông góc AH xuống BC và AK xuống CD.

  • Giải bài tập 4.21 trang 90 SGK Toán 9 tập 1 - Cùng khám phá

    Cho tam giác vuông có góc nhọn \(\alpha \). Tỉ số giữa cạnh đối và cạnh kề của góc \(\alpha \) là A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \).

  • Giải bài tập 4.22 trang 90 SGK Toán 9 tập 1 - Cùng khám phá

    Tam giác ABC vuông tại A có \(AB = 10cm,BC = 15cm\). Khi đó, sinB bằng A. \(\frac{{\sqrt 5 }}{3}\). B. \(\frac{{\sqrt 3 }}{5}\). C. \(\frac{3}{5}\). D. \(\frac{5}{3}\).

  • Giải bài tập 4.23 trang 90 SGK Toán 9 tập 1 - Cùng khám phá

    Góc nhọn \(\alpha \) có \(\cot \alpha = \sqrt 3 \). Số đo của góc \(\alpha \) là A. \({30^o}\). B. \({60^o}\). C. \({45^o}\). D. \({75^o}\).

  • Giải bài tập 4.24 trang 90 SGK Toán 9 tập 1 - Cùng khám phá

    Trong Hình 4.35, tỉ số \(\frac{{BC}}{{AH}}\) bằng A. \(\frac{{\sqrt 3 }}{3} + 1\). B. \(\sqrt 3 + 1\). C. \(\frac{{\sqrt 2 }}{2} + 1\). D. \(\sqrt 2 + 1\).

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store