 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 1. Vecto trong không gian - Toán 12 Cùng khám phá
Bài 1. Vecto trong không gian - Toán 12 Cùng khám phá
Giải bài tập 2.2 trang 54 SGK Toán 12 tập 1 - Cùng khám phá
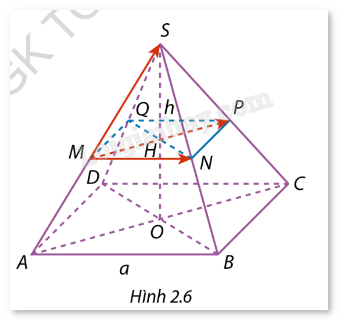
Cho hình chóp đều S.ABCD có cạnh đáy \(a\) và đường cao \(h\). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD và O, H lần lượt là tâm của các hình vuông ABCD, MNPQ (Hình 2.6). a) Trong những vectơ khác \(\vec O\), có điểm đầu và điểm cuối là những điểm cho trên hình, hãy liệt kê các vectơ: - Cùng hướng với \(\overrightarrow {MN} \); - Bằng \(\overrightarrow {MN} \). b) Tìm độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \) theo \(a\) và \(h\).
Đề bài
Cho hình chóp đều S.ABCD có cạnh đáy
\(a\) và đường cao \(h\). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD và O, H lần lượt là tâm của các hình vuông ABCD, MNPQ (Hình 2.6).
a) Trong những vectơ khác \(\vec O\), có điểm đầu và điểm cuối là những điểm cho trên hình, hãy liệt kê các vectơ:
- Cùng hướng với \(\overrightarrow {MN} \);
- Bằng \(\overrightarrow {MN} \).
b) Tìm độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \) theo \(a\) và \(h\).
Phương pháp giải - Xem chi tiết
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết
a) Liệt kê các vectơ
- Cùng hướng với \(\overrightarrow {MN} \):
Vectơ cùng hướng với \(\overrightarrow {MN} \) là các vectơ có phương và chiều giống với \(\overrightarrow {MN} \), cụ thể là: \(\overrightarrow {QP} \), \(\overrightarrow {AB} \), \(\overrightarrow {DC} \).
- Bằng \(\overrightarrow {MN} \):
Vectơ bằng \(\overrightarrow {MN} \) là các vectơ có độ dài và phương chiều giống với \(\overrightarrow {MN} \), cụ thể là: \(\overrightarrow {QP} \)
b) Tính độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \)
- Tính độ dài \(\overrightarrow {MP} \):
Ta xét tam giác đều SAC có MP là đường trung bình của tam giác đều SAC
\(MP = \frac{1}{2}AC = \frac{1}{2} \cdot a\sqrt 2 \) (AC là đường chéo của hình vuông ABCD)
Do đó: \(\overrightarrow {MP} = \frac{{a\sqrt 2 }}{2}\)
- Tính độ dài \(\overrightarrow {MS} \):
Ta xét tam giác vuông SOA với \(O\) là tâm của hình vuông đáy ABCD:
\(SA = \sqrt {{h^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \sqrt {{h^2} + \frac{{{a^2}}}{2}} \)
Vì \(M\) là trung điểm của SA, ta có: \(SM = \frac{1}{2}SA = \frac{1}{2}\sqrt {{h^2} + \frac{{{a^2}}}{2}} \)
Do đó: \(\overrightarrow {MS} = \frac{1}{2}\sqrt {{h^2} + \frac{{{a^2}}}{2}} \)
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận