 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 1. Tính đơn điệu và cực trị của hàm số - Toán 12 Cù..
Bài 1. Tính đơn điệu và cực trị của hàm số - Toán 12 Cù..
Giải bài tập 1.7 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
Thể tích \(V\) của 1 kg nước (tính bằng cm3¬) ở nhiệt độ \(T\) (đơn vị: oC) khi \(T\) thay đổi từ 0oC đến 30oC được cho xấp xỉ bởi công thức: \(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\) (Nguồn: James Stewart,J(2015).Calculus.Cengage Learning 8th edition, p.284) Tìm nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng( làm tròn kết quả đến hàng đơn vị
Đề bài
Thể tích \(V\) của 1 kg nước (tính bằng cm3) ở nhiệt độ \(T\) (đơn vị: oC) khi \(T\) thay đổi từ 0oC đến 30oC được cho xấp xỉ bởi công thức:
\(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\)
(Nguồn: James Stewart,J(2015).Calculus.Cengage Learning 8th edition, p.284)
Tìm nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng( làm tròn kết quả đến hàng đơn vị
Phương pháp giải - Xem chi tiết
Nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng là tìm khoảng dông biến của hàm số \(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\)
Bước 1: Tính
Bước 2: Lập bảng biến thiên
Bước 3: Xác định khoảng dông biến của hàm số dựa vào bảng biến thiên
Lời giải chi tiết
Ta có: \(V' = - 0,06426 + 2.0,0085043T - 3.0,0000769{T^2}\)
Xét \(V' = 0\)\( \Rightarrow - 0,06426 + 2.0,0085043T - 3.0,0000769{T^2} = 0\)
\( \Rightarrow \left[ \begin{array}{l}T = 69\\T = 4\end{array} \right.\)
Từ đó ta có bảng biến thiên là
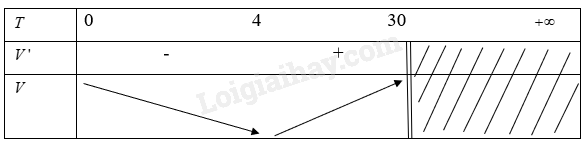
Từ bảng biến thiên ta thấy
Hàm số trên đồng biến từ \({T_0} = 4\)hay thể tích nước tăng từ khi \({T_0} = 4\)
- Giải bài tập 1.8 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.4 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.6 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.5 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.3 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận