Giải bài tập 11 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo

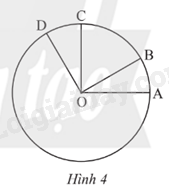
Quan sát Hình 4. Biết (widehat {DOA} = {120^o}), OA ( bot )OC, OB ( bot )OD. a) Đọc tên các góc ở tâm có trong hình. b) Tính số đo của mỗi góc ở tâm tìm được ở câu a c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o d) So sánh hai cung nhỏ (oversetfrown{AB}) và (oversetfrown{CD}).

Đề bài

Quan sát Hình 4. Biết \(\widehat {DOA} = {120^o}\), OA \( \bot \)OC, OB \( \bot \)OD.

a) Đọc tên các góc ở tâm có trong hình.

b) Tính số đo của mỗi góc ở tâm tìm được ở câu a

c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180^o

d) So sánh hai cung nhỏ \(\overset\frown{AB}\) và \(\overset\frown{CD}\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào: Góc ở tâm là góc có đỉnh trùng với tâm đường tròn, dựa vào hình để xác định góc.

Lời giải chi tiết

a) Các góc ở tâm có trong hình là: \(\widehat {DOA};\widehat {DOC};\widehat {COB};\widehat {BOA};\widehat {DOB};\widehat {COA}\)

b) Ta có: \(\widehat {DOA} = {120^o}\)

Vì \(OA \bot OC\) nên \(\widehat {COA} = {90^o}\)

Vì \(OB \bot OD\) nên \(\widehat {DOB} = {90^o}\)

Từ đó ta tính được:

\(\widehat {DOC} = \widehat {DOA} - \widehat {COA} = {120^o} - {90^o} = {30^o}\)

\(\widehat {COB} = \widehat {DOB} - \widehat {DOC} = {90^o} - {30^o} = {60^o}\)

\(\widehat {BOA} = \widehat {COA} - \widehat {COB} = {90^o} - {60^o} = {30^o}\)

c) sđ\(\overset\frown{CD}=\) sđ\(\overset\frown{AB}\) \((= 30^o)\)

sđ\(\overset\frown{BD}=\) sđ\(\overset\frown{AC}\) \(( = 90^o)\)

d) sđ\(\overset\frown{AB}\) = sđ\(\overset\frown{CD}\) \((=30^o)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 12 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng a) AC vuông góc với DC b) (widehat {ABC} = widehat {ADC}) c) AB. AC = AH. AD
Giải bài tập 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hãy hoàn thành bảng số liệu sau và vở (lấy (pi approx 3,14) và làm tròn kết quả đến hàng phần mười)
Giải bài tập 14 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC. a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài B. b) Gọi H là trung điểm AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi. c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng. d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).
Giải bài tập 15 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyên Hàm Thuận Nam, tỉnh Bình Thuận. Biết ngọn hải đăng cao 65 m so với mặt nước biển. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng này? Cho biết mắt người quan sát ở độ cao 5 m so với mực nước biển và bán kính Trái Đất gần bằng 6400 km.
Giải bài tập 10 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) có diện tích bằng A. (12c{m^2}) B. (24c{m^2}) C. (4pi c{m^2}) D. (12pi c{m^2})
Giải bài tập 9 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hình quạt tròn bán kính R, ứng với cung 90o có diện tích bằng A. (pi {R^2}) B. (frac{{pi {R^2}}}{2}) C. (frac{{pi {R^2}}}{4}) D. (frac{{pi {R^2}}}{8})
Giải bài tập 8 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong một đường tròn, khẳng định nào sau đây là sai? A. Các góc nội tiếp chắn nửa đường tròn là góc vuông. B. Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau. C. Hai góc nội tiếp cùng chắn một cung thì bằng nhau. D. Hai góc nội tiếp bằng nhau thì cùng chắn một cung.
Giải bài tập 7 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong Hình 3, (widehat {ACB}) là góc A. vuông B. tù C. nhọn D. bẹt
Giải bài tập 6 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M (Hình 2). Biết (widehat {AMB} = {50^o}). Số đo cung nhỏ AB là: A. 140o B. 230o C. 130o D. 150o
Giải bài tập 5 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo
Góc nội tiếp chắn nửa đường tròn có số đo là: A. 180o B. 120o C. 90o D. 60o
Giải bài tập 4 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hình nào dưới đây biểu diễn góc nội tiếp? A. Hình 1a B. Hình 1b C. Hình 1c D. Hình 1d
Giải bài tập 3 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo
Góc ở tâm là góc A. có đỉnh nằm trên đường tròn B. có đỉnh nằm trên bán kính của đường tròn. C. có hai cạnh là hai đường kính của đường tròn. D. có đỉnh trùng tâm đường tròn.
Giải bài tập 2 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho đường tròn (O; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4 cm. Kết luận nào sau đây đúng về vị trí giữa đường tròn (O) và đường thẳng a? A. (O) và a cắt nhau tại hai điểm. B. (O) và a tiếp xúc. C. (O) và a không có điểm chung. D. (O) và a có duy nhất điểm chung.
Giải bài tập 1 trang 103 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hai đường tròn (O; 5 cm), (O’; 4 cm) với OO’ = 9 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn? A. Hai đường tròn cắt nhau. B. Hai đường tròn ở ngoài nhau. C. Hai đường tròn tiếp xúc ngoài. D. Hai đường tròn tiếp xúc trong.