SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống Bài 27. Thể tích - SBT Toán 11 KNTT

Giải bài 7.35 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống


Cho hình lăng trụ \(ABC \cdot A'B'C'\) có \(A'B'C'\) và \(AA'C'\) là hai tam giác đều cạnh \(a\).

Đề bài

Cho hình lăng trụ \(ABC \cdot A'B'C'\) có \(A'B'C'\) và \(AA'C'\) là hai tam giác đều cạnh \(a\). Biết \(\left( {ACC'A'} \right) \bot \left( {A'B'C'} \right)\). Tính theo \(a\) thể tích khối lăng trụ \(ABC \cdot A'B'C'\).

Phương pháp giải - Xem chi tiết

Áp dụng công thức tính thể tích khối lăng trụ: \(S = B.h\).

Trong đó: \(B\) là diện tích đa giác đáy

\(h\) là đường cao của hình lăng trụ

Lời giải chi tiết

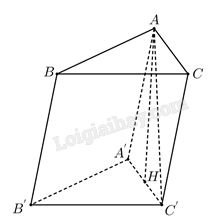
Kẻ \(AH \bot A'C'\) tại \(H\) thì \(AH \bot \left( {A'B'C'} \right)\).

Ta có \({S_{A'B'C'}} = \frac{{{a^2}\sqrt 3 }}{4};AH = \frac{{a\sqrt 3 }}{2}\)

Suy ra \({V_{ABC.A'B'C'}} = {S_{A'B'C'}} \cdot AH\)\( = \frac{{{a^2}\sqrt 3 }}{4} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{3{a^3}}}{8}\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store