SBT Toán 8 - giải SBT Toán 8 - Chân trời sáng tạo Bài 2. Các trường hợp đồng dạng của hai tam giác - SBT ..

Giải bài 7 trang 63 sách bài tập toán 8 - Chân trời sáng tạo tập 2


Cho tam giác ABC có \(AB = 12,AC = 15\). Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho \(AM = 7,5,AN = 6\).

Đề bài

Cho tam giác ABC có \(AB = 12,AC = 15\). Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho \(AM = 7,5,AN = 6\). Chứng minh rằng:

a) $\Delta ANM\backsim \Delta ABC$.

b) \(\widehat {ABN} = \widehat {ACM}\).

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.

Lời giải chi tiết

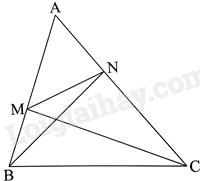
a) Tam giác ANM và tam giác ABC có:

\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} = \frac{1}{2},\widehat A\;chung\) nên $\Delta ANM\backsim \Delta ABC\left( c.g.c \right)$

b) Vì \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\) nên \(\frac{{AN}}{{AM}} = \frac{{AB}}{{AC}}\) và \(\widehat A\;chung\)

Do đó, $\Delta ANB\backsim \Delta AMC\left( c.g.c \right)$ nên \(\widehat {ABN} = \widehat {ACM}\)


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store