Giải Bài 3 trang 65 sách bài tập toán 7 - CTST

Cho tam giác ABC có M là giao điểm của hai đường phân giác của góc B và góc C. Cho biết \(\widehat {BMC} = {132^o}\). Tính số đo các góc \(\widehat {MAB}\) và \(\widehat {MAC}\).

Đề bài

Cho tam giác ABC có M là giao điểm của hai đường phân giác của góc B và góc C. Cho biết \(\widehat {BMC} = {132^o}\). Tính số đo các góc \(\widehat {MAB}\) và \(\widehat {MAC}\).

Phương pháp giải - Xem chi tiết

Sử dụng tính chất tia phân giác của các góc trong một tam giác để tính số đo góc cần tìm.

Lời giải chi tiết

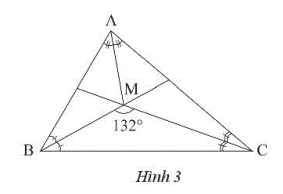
Ta có \(\widehat {MBC} + \widehat {MCB} = {180^o} - \widehat {BMC} = {180^o} - {132^o} = {48^o}\)

Do BM và CM là phân giác các góc \(\widehat B\) và \(\widehat C\) của tam giác ABC nên ta có:

\(\widehat B + \widehat C = 2\left( {\widehat {MBC} + \widehat {MCB}} \right) = {2.48^o} = {96^o}\)

Suy ra: \(\widehat {{A^{}}} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {96^o} = {84^o}\)

Do AM là phân giác của góc A của tam giác ABC nên ta có:

\(\widehat {MAB} = \widehat {MAC} = \frac{{\widehat {{A^{}}}}}{2} = \frac{{{{84}^o}}}{2} = {42^o}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải Bài 4 trang 65 sách bài tập toán 7 - CTST
Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.
Giải Bài 5 trang 65 sách bài tập toán 7 - CTST
Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho \(MA + MB + MC + M{\rm{D}}\) nhỏ nhất.
Giải Bài 6 trang 65 sách bài tập toán 7 - CTST
a) Chứng minh trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh.
Giải Bài 7 trang 66 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng \(\widehat {BIH} = \widehat {CI{\rm{D}}}\).
Giải Bài 8 trang 66 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC cân tại A và cho \(\widehat {{A^{}}} = {124^o}\). Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK.
Giải Bài 9 trang 66 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.
Giải Bài 10 trang 66 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác nhọn ABC. Hãy nêu cách tìm các điểm sau đây bên trong tam giác ABC.
Giải Bài 2 trang 65 sách bài tập toán 7 - CTST
Cho tam giác ABC có M là điểm đồng quy của ba đường phân giác. Qua M vẽ đường thẳng song song với Bc và cắt AB, AC lần lượt tại N và P. Chứng minh rằng NP = BN + CP.
Giải Bài 1 trang 65 sách bài tập toán 7 - CTST
Cho tam giác ABC có \(\widehat {{A^{}}} = \widehat B + \widehat C\). Hai đường phân giác của góc B và góc C cắt nhau tại O.