Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 29 trang 161 SBT toán 9 tập 1


Giải bài 29 trang 161 sách bài tập toán 9. Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:...

Đề bài

Cho đường tròn \((O),\) hai dây \(AB, CD\) bằng nhau và cắt nhau tại điểm \(I\) nằm bên trong đường tròn. Chứng minh rằng:

\(a)\) \(IO\) là tia phân giác của một trong hai góc tạo bởi hai dây \(AB\) và \(CD.\)

\(b)\) Điểm \(I\) chia \(AB,\) \(CD\) thành các đoạn thẳng bằng nhau đôi một. 

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức: Trong một đường tròn:

+) Hai dây bằng nhau thì cách đều tâm.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Lời giải chi tiết

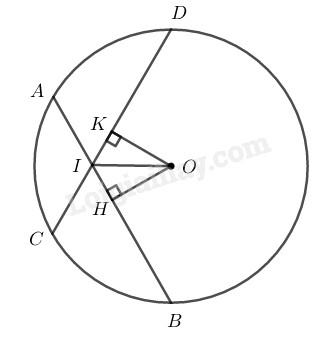
\(a)\) Kẻ \(OH ⊥ AB,\) \(OK ⊥ CD\)

Ta có: \(AB = CD\;\; (gt)\)

Suy ra: \(OH = OK\) (hai dây bằng nhau cách đều tâm)

Do đó O nằm trên tia phân giác của góc BID (tính chất đường phân giác)

Vậy \(IO\) là tia phân giác của góc \(BID\) 

\(b)\) Xét hai tam giác \(OIH\) và \(OIK,\) ta có:

+) \(\widehat {OHI} = \widehat {OKI} = 90^\circ \)

+) \(OI\) chung

+) \(OH = OK\) (chứng minh trên)

Suy ra: \(∆OIH = ∆OIK\) (cạnh huyền, cạnh góc vuông)

Suy ra: \(IH = IK      \;(1)\)

Xét (O) có \(OH ⊥ AB\) nên \(HA = HB = \displaystyle {1 \over 2}AB\) (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Xét (O) có \(OK ⊥ DC\) nên \(KC = KD =\displaystyle {1 \over 2}CD\) (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Mà \(AB = CD\) (gt) nên \(HA = KC\;\) hay \(AI+IH=IC+IK\) mà \(IH=IK\) (theo (1))

Suy ra: \(IA = IC\)

Ta lại có \(AB= CD\) (gt) hay \(IA+IB=IC+ID\) mà \(IA=IC\) (cmt) nên \(IB = ID.\)

Vậy \(IA=IC, IB=ID\). 

Loigiaihay.com


Bình chọn:
4.6 trên 14 phiếu
Bài tiếp theo
  • Bài 30 trang 161 SBT toán 9 tập 1

    Giải bài 30 trang 161 sách bài tập toán 9. Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.

  • Bài 31 trang 161 SBT toán 9 tập 1

    Giải bài 31 trang 161 sách bài tập toán 9. Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:...

  • Bài 32* trang 161 SBT toán 9 tập 1

    Giải bài 32* trang 161 sách bài tập toán 9. Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm...

  • Bài 33* trang 161 SBT toán 9 tập 1

    Giải bài 33* trang 161 sách bài tập toán 9. Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB >CD, chứng minh rằng MH > MK.

  • Bài 34* trang 161 SBT toán 9 tập 1

    Giải bài 34* trang 161 sách bài tập toán 9. Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store