Giải bài 27 trang 81 sách bài tập toán 11 - Cánh diều

Cho đồ thị hàm số \(y = f\left( x \right)\) trong hình dưới đây. Phát biểu nào sau đây là SAI?

Đã có lời giải SGK Toán lớp 12 - Cánh diều (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho đồ thị hàm số \(y = f\left( x \right)\) trong hình dưới đây. Phát biểu nào sau đây là SAI?

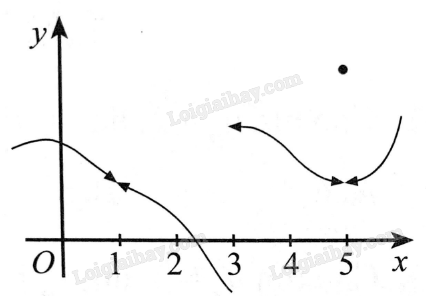
A. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 1\).

B. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 3\).

C. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 5\).

D. Hàm số \(y = f\left( x \right)\) không liên tục tại \(x = 0\).

Phương pháp giải - Xem chi tiết

Sử dụng định nghĩa hàm số liên tục tại một điểm.

Lời giải chi tiết

Nhìn vào đồ thị, ta thấy:

+ \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\), nhưng trên hình vẽ ta thấy \(f\left( 1 \right)\) không tồn tại, nên hàm số không liên tục tại \(x = 1\).

+ \(\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right)\) nên hàm số không liên tục tại \(x = 3\).

+ \(\mathop {\lim }\limits_{x \to {5^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {5^ + }} f\left( x \right) \ne f\left( 5 \right)\) nên hàm số không liên tục tại \(x = 5\).

+ \(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = f\left( 0 \right)\) nên hàm số liên tục tại \(x = 0\).

Đáp án cần chọn là đáp án D.