Đề thi học kì 1 Toán 12 - Đề số 10
Đề thi học kì 1 Toán 12 - Đề số 10
Đề bài
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( {0; + \infty } \right)\)
-
B.
\(\left( { - 3;0} \right)\)
-
C.
\(\left( {0;2} \right)\)
-
D.
\(\left( { - \infty ; - 3} \right)\)
Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có $f'(x) = (x - 1)^2 \left( x^2 - 5x + 6 \right)$. Số điểm cực trị của hàm số đã cho là
-
A.
3.
-
B.
5.
-
C.
2.
-
D.
4.
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\backslash \{ 1\} \) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f(x) là

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ:

Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = {x^3} - 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} - 1\)
Cho ba điểm M, N, P tùy ý. Khẳng định nào sau đây đúng?
-
A.
$\overset{\rightarrow}{MN} + \overset{\rightarrow}{NP} = \overset{\rightarrow}{MP}$.
-
B.
$\overset{\rightarrow}{MN} - \overset{\rightarrow}{NP} = \overset{\rightarrow}{MP}$.
-
C.
$\overset{\rightarrow}{PN} - \overset{\rightarrow}{PM} = \overset{\rightarrow}{NM}$.
-
D.
$\overset{\rightarrow}{MP} + \overset{\rightarrow}{PN} = \overset{\rightarrow}{0}$.
Cho hình lập phương $ABCD.EFGH$. Số đo góc giữa hai vectơ $\overset{\rightarrow}{AD}$ và $\overset{\rightarrow}{BG}$ là
-
A.
$30{^\circ}$.
-
B.
$45{^\circ}$.
-
C.
$90{^\circ}$.
-
D.
$135{^\circ}$.
Trong không gian Oxy, cho vecto \(\overrightarrow {OM} = 2\overrightarrow i - 3\overrightarrow j + 4\overrightarrow k \). Tọa độ của điểm M là
-
A.
\((2; - 3;4)\)
-
B.
\((2;4; - 3)\)
-
C.
\((2;3;4)\)
-
D.
\(( - 2;3; - 4)\)
Trong không gian Oxyz, cho điểm M(4;1;3). Điểm M’ đối xứng với M qua mặt phẳng (Oxz) có tọa độ
-
A.
(-4;-1;3)
-
B.
(-4;-1;-3)
-
C.
(4;-1;3)
-
D.
(4;1;-3)
Trong không gian Oxy, cho hai vecto \(\overrightarrow u = (1;3; - 2)\) và \(\overrightarrow v = (2;1; - 1)\). Tọa độ của vecto \(\overrightarrow u - \overrightarrow v \) là
-
A.
(3;4;-3)
-
B.
(-1;2;-3)
-
C.
(-1;2;-1)
-
D.
(1;-2;1)
Trong không gian Oxyz, gọi A’ là hình chiếu vuông góc của điểm A(1;2;3) lên mặt phẳng (Oyz). Tọa độ vecto \(\overrightarrow {AA'} \) là
-
A.
(0;2;3)
-
B.
(-1;0;0)
-
C.
(1;0;0)
-
D.
(0;2;0)
Thời gian hoàn thành bài kiểm tra cuối học kỳ II môn Toán của các bạn học sinh lớp 12A được cho trong bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
-
A.
25.
-
B.
20.
-
C.
30.
-
D.
15.
Một mẫu số liệu ghép nhóm có tứ phân vị là \({Q_1} = 3\), \({Q_2} = 5\), \({Q_3} = 9\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
-
A.
2
-
B.
4
-
C.
5
-
D.
6
Một sân vận động với sân bóng phẳng hình chữ nhật có chấm trắng trung tâm là nơi giao bóng, một đường kẻ vạch chia đôi sân và các khán đài. Khán đài A gồm những dãy ghế nằm vuông góc với vạch chia đôi sân có độ cao tăng dần (các ghế cùng hàng thì cùng độ cao so với mặt sân). Chọn hệ trục tọa độ Oxyz sao cho O trùng với điểm giao bóng, mặt phẳng Oxy trùng với mặt sân, trục Ox trùng với vạch chia đôi sân, tia Oz vuông góc với mặt sân (đơn vị đo lấy theo mét).
Một khán giả ngồi tại vị trí M của khán đài A, có hình chiếu vuông góc lên mặt phẳng chứa sân là một điểm thuộc Ox. Góc hợp bởi OM và mặt sân là $\alpha$ với $\sin\alpha = \dfrac{1}{3}$, nếu người này di chuyển 10 (m) trên hàng ngang đó đến ngồi tại một vị trí N thì góc hợp bởi ON và mặt sân là $\beta$ với $\sin\beta = \dfrac{\sqrt{10}}{10}$. Gọi h (m) là độ cao tại M so với mặt sân.

a) Điểm M có cao độ bằng 0.
b) Điểm N có cùng tung độ với điểm M.
c) OM = 3h.
d) h = 10 m.
Tìm hiểu về số giờ nắng/ngày (tính theo hiệu suất của tấm pin năng lượng mặt trời thu được trong một ngày) vào tháng 9/2024 để theo dõi sản lượng điện mặt trời mái nhà của một hộ dân tại TP Buôn Ma Thuột, thu được bảng số liệu sau:

a) Số giờ nắng/ngày trung bình của bảng số liệu này (làm tròn đến hàng phần trăm) là 3,57.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm này là 5.
c) Phương sai của mẫu số liệu ghép nhóm trên (làm trong đến hàng phần chục) là $s^{2} = 3,2$.
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm này là $2,75$.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 2\) cắt đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x + m\) tại 3 điểm phân biệt?
Một sân điền kinh gồm hai sân hình bán nguyệt có bán kính x (m, x > 0) và một sân hình chữ nhật như hình vẽ. Biết chu vi của sân điền kinh là 400 m, tìm diện tích lớn nhất của sân hình chữ nhật theo mét vuông (làm tròn kết quả đến hàng đơn vị).

Theo định luật II: Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật: $\overrightarrow{F} = m\overrightarrow{a}$, trong đó $\overrightarrow{F}$ là vecto lực (N), $\overrightarrow{a}$ là vector gia tốc $(m/s^2)$, m (kg) là khối lượng của vật. Muốn truyền cho quả bóng có khối lượng 0,5 (kg) một gia tốc 50 $(m/{{s}^{2}})$ thì cần một lực đá có độ lớn là bao nhiêu?

Hình dưới đây mô tả một sân cầu lông với kích thước theo tiêu chuẩn quốc tế. Ta chọn hệ trục Oxyz cho sân đó (đơn vị trên mỗi trục là mét) và hai điểm A, B như hình. Khi đó, tọa độ của , hãy tính: a + b + c (kết quả làm tròn đến hàng phần trăm).

Lời giải và đáp án
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( {0; + \infty } \right)\)
-
B.
\(\left( { - 3;0} \right)\)
-
C.
\(\left( {0;2} \right)\)
-
D.
\(\left( { - \infty ; - 3} \right)\)
Đáp án : B
Hàm số y = f(x) nghịch biến trên khoảng f’(x) < 0.
Hàm số nghịch biến trên khoảng (-3;0) vì f’(x) < 0 trên (-3;0).
Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có $f'(x) = (x - 1)^2 \left( x^2 - 5x + 6 \right)$. Số điểm cực trị của hàm số đã cho là
-
A.
3.
-
B.
5.
-
C.
2.
-
D.
4.
Đáp án : C
Tìm số nghiệm bội lẻ của phương trình y = f'(x).
\(f'(x) = {(x - 1)^2}({x^2} - 5x + 6) = {(x - 1)^2}(x - 2)(x - 3)\).
Phương trình f’(x) = 0 có hai nghiệm bội lẻ là x = 2 và x = 3 nên hàm số f(x) có hai điểm cực trị.
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\backslash \{ 1\} \) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = f(x) là

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Ta có $\lim_{x \to 1^+} y = -\infty$; $\lim_{x \to 1^-} x = +\infty $ nên ta có một tiệm cận đứng là $x=1$.
Mặt khác $\lim_{x \to +\infty} y = -1$; $\lim_{x \to -\infty} y = 1 $ nên ta có hai tiệm cận ngang là $y=1$ và $y=-1$.
Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ:

Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = {x^3} - 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} - 1\)
Đáp án : B
Quan sát bảng biến thiên, tìm đạo hàm, xét các điểm cực trị và các giá trị của hàm số tại điểm đó, thay số vào f(x), f’(x) để tìm các hệ số của phương trình.
Ta có: \(f'(x) = 3a{x^2} + 2bx + c\). Đồ thị đạt cực trị tại các điểm (0;1) và (-2;-3) nên f’(0) = 0, f’(-2) = 0.
Đồ thị hàm số đi qua các điểm (-2;-3) và (0;1) nên f(-2) = -3, f(0) = 1.
Ta có hệ phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{f'(0) = 0}\\{f(0) = 1}\\{f'( - 2) = 0}\\{f( - 2) = - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{12a - 4b = 0}\\{ - 8a + 4b + 1 = - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{a = - 1}\\{b = - 3}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^3} - 3{x^2} + 1\).
Cho ba điểm M, N, P tùy ý. Khẳng định nào sau đây đúng?
-
A.
$\overset{\rightarrow}{MN} + \overset{\rightarrow}{NP} = \overset{\rightarrow}{MP}$.
-
B.
$\overset{\rightarrow}{MN} - \overset{\rightarrow}{NP} = \overset{\rightarrow}{MP}$.
-
C.
$\overset{\rightarrow}{PN} - \overset{\rightarrow}{PM} = \overset{\rightarrow}{NM}$.
-
D.
$\overset{\rightarrow}{MP} + \overset{\rightarrow}{PN} = \overset{\rightarrow}{0}$.
Đáp án : A
Áp dụng quy tắc ba điểm.
Theo quy tắc ba điểm, ta có $\overset{\rightarrow}{MN} + \overset{\rightarrow}{NP} = \overset{\rightarrow}{MP}$.
Cho hình lập phương $ABCD.EFGH$. Số đo góc giữa hai vectơ $\overset{\rightarrow}{AD}$ và $\overset{\rightarrow}{BG}$ là
-
A.
$30{^\circ}$.
-
B.
$45{^\circ}$.
-
C.
$90{^\circ}$.
-
D.
$135{^\circ}$.
Đáp án : B
Trong không gian, cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne \overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \). Khi đó, \(\widehat {AOB}\) \(\left( {{0^o} < \widehat {AOB} < {{180}^o}} \right)\) được gọi là góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).

\(\left( {\overrightarrow {AD} ;\overrightarrow {BG} } \right) = \left( {\overrightarrow {BC} ;\overrightarrow {BG} } \right) = \widehat {CBG} = {45^o}\).
Trong không gian Oxy, cho vecto \(\overrightarrow {OM} = 2\overrightarrow i - 3\overrightarrow j + 4\overrightarrow k \). Tọa độ của điểm M là
-
A.
\((2; - 3;4)\)
-
B.
\((2;4; - 3)\)
-
C.
\((2;3;4)\)
-
D.
\(( - 2;3; - 4)\)
Đáp án : A
\(\overrightarrow a = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = (m;n;p)\).
\(\overrightarrow {OM} = 2\overrightarrow i - 3\overrightarrow j + 4\overrightarrow k = (2; - 3;4)\).
Trong không gian Oxyz, cho điểm M(4;1;3). Điểm M’ đối xứng với M qua mặt phẳng (Oxz) có tọa độ
-
A.
(-4;-1;3)
-
B.
(-4;-1;-3)
-
C.
(4;-1;3)
-
D.
(4;1;-3)
Đáp án : C
Điểm M’ đối xứng với M(a;b;c) qua mặt phẳng (Oxz) có tọa độ M’(a;-b;c).
Điểm M’ đối xứng với M(4;1;3) qua mặt phẳng (Oxz) có tọa độ M’(4;-1;3).
Trong không gian Oxy, cho hai vecto \(\overrightarrow u = (1;3; - 2)\) và \(\overrightarrow v = (2;1; - 1)\). Tọa độ của vecto \(\overrightarrow u - \overrightarrow v \) là
-
A.
(3;4;-3)
-
B.
(-1;2;-3)
-
C.
(-1;2;-1)
-
D.
(1;-2;1)
Đáp án : C
\(\overrightarrow u - \overrightarrow v = ({x_u} - {x_v};{y_u} - {y_v};{z_u} - {z_v})\).
\(\overrightarrow u - \overrightarrow v = (1 - 2;3 - 1; - 2 + 1) = ( - 1;2; - 1)\).
Trong không gian Oxyz, gọi A’ là hình chiếu vuông góc của điểm A(1;2;3) lên mặt phẳng (Oyz). Tọa độ vecto \(\overrightarrow {AA'} \) là
-
A.
(0;2;3)
-
B.
(-1;0;0)
-
C.
(1;0;0)
-
D.
(0;2;0)
Đáp án : B
Hình chiếu của điểm M(a;b;c) lên mặt phẳng (Oyz) là điểm M’(0;b;c).
Ta có A’(0;2;3) suy ra \(\overrightarrow {AA'} = (0 - 1;2 - 2;3 - 3) = ( - 1;0;0)\).
Thời gian hoàn thành bài kiểm tra cuối học kỳ II môn Toán của các bạn học sinh lớp 12A được cho trong bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
-
A.
25.
-
B.
20.
-
C.
30.
-
D.
15.
Đáp án : A
Lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên (chứa mẫu số liệu).
Khoảng biến thiên: \(R = 90 - 65 = 25\).
Một mẫu số liệu ghép nhóm có tứ phân vị là \({Q_1} = 3\), \({Q_2} = 5\), \({Q_3} = 9\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
-
A.
2
-
B.
4
-
C.
5
-
D.
6
Đáp án : D
Khoảng tứ phân vị của mẫu số liệu ghép nhóm được tính bởi công thức: \({\Delta _Q} = {Q_3} - {Q_1}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \({\Delta _Q} = {Q_3} - {Q_1} = 9 - 3 = 6\).
Một sân vận động với sân bóng phẳng hình chữ nhật có chấm trắng trung tâm là nơi giao bóng, một đường kẻ vạch chia đôi sân và các khán đài. Khán đài A gồm những dãy ghế nằm vuông góc với vạch chia đôi sân có độ cao tăng dần (các ghế cùng hàng thì cùng độ cao so với mặt sân). Chọn hệ trục tọa độ Oxyz sao cho O trùng với điểm giao bóng, mặt phẳng Oxy trùng với mặt sân, trục Ox trùng với vạch chia đôi sân, tia Oz vuông góc với mặt sân (đơn vị đo lấy theo mét).
Một khán giả ngồi tại vị trí M của khán đài A, có hình chiếu vuông góc lên mặt phẳng chứa sân là một điểm thuộc Ox. Góc hợp bởi OM và mặt sân là $\alpha$ với $\sin\alpha = \dfrac{1}{3}$, nếu người này di chuyển 10 (m) trên hàng ngang đó đến ngồi tại một vị trí N thì góc hợp bởi ON và mặt sân là $\beta$ với $\sin\beta = \dfrac{\sqrt{10}}{10}$. Gọi h (m) là độ cao tại M so với mặt sân.

a) Điểm M có cao độ bằng 0.
b) Điểm N có cùng tung độ với điểm M.
c) OM = 3h.
d) h = 10 m.
a) Điểm M có cao độ bằng 0.
b) Điểm N có cùng tung độ với điểm M.
c) OM = 3h.
d) h = 10 m.
Quan sát hình vẽ và xác định tọa độ các điểm.
Gọi K là hình chiếu của N trên (Oxy).
Áp dụng hệ thức lượng trong tam giác vuông và định lí Pythagore để tính.
a) Sai. Điểm M không thuộc (Oxy) nên cao độ khác 0.
b) Sai. Điểm M có tung độ bằng 0 và điểm N có tung độ khác 0.
c) Đúng. \(\alpha = \left( {OM,(Oxy)} \right) = \left( {OM,OH} \right) = \widehat {MOH}\).
Xét tam giác MHN vuông tại H:
\(\sin \alpha = \frac{{MH}}{{OM}} \Leftrightarrow OM = \frac{{MH}}{{\sin \alpha }} = \frac{h}{{\frac{1}{3}}} = 3h\).
d) Đúng. Gọi K là hình chiếu của N trên (Oxy).
\(\beta = \left( {ON,(Oxy)} \right) = \left( {ON,OK} \right) = \widehat {NOK}\).
Xét tam giác NOK vuông tại K:
\(\sin \beta = \frac{{\sqrt {10} }}{{10}} \Leftrightarrow \frac{h}{{ON}} = \frac{{\sqrt {10} }}{{10}} \Leftrightarrow ON = h\sqrt {10} \).
Xét tam giác MON vuông tại M:
\(\sqrt {O{N^2} - O{M^2}} = MN \Leftrightarrow \sqrt {10{h^2} - 9{h^2}} = 10 \Leftrightarrow h = 10\) (m).
Tìm hiểu về số giờ nắng/ngày (tính theo hiệu suất của tấm pin năng lượng mặt trời thu được trong một ngày) vào tháng 9/2024 để theo dõi sản lượng điện mặt trời mái nhà của một hộ dân tại TP Buôn Ma Thuột, thu được bảng số liệu sau:

a) Số giờ nắng/ngày trung bình của bảng số liệu này (làm tròn đến hàng phần trăm) là 3,57.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm này là 5.
c) Phương sai của mẫu số liệu ghép nhóm trên (làm trong đến hàng phần chục) là $s^{2} = 3,2$.
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm này là $2,75$.
a) Số giờ nắng/ngày trung bình của bảng số liệu này (làm tròn đến hàng phần trăm) là 3,57.
b) Khoảng biến thiên của mẫu số liệu ghép nhóm này là 5.
c) Phương sai của mẫu số liệu ghép nhóm trên (làm trong đến hàng phần chục) là $s^{2} = 3,2$.
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm này là $2,75$.
Khoảng biến thiên, kí hiệu R, của mẫu số liệu ghép nhóm là hiếu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu của mẫu số liệu.
Phương sai:
- Công thức 1: \({S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\).
- Công thức 2: \({S^2} = \frac{1}{n}\left( {{n_1}{c_1}^2 + {n_2}{c_2}^2 + ... + {n_k}{c_k}^2} \right) - {\overline x ^2}\).
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu; \(\overline x = \frac{1}{n}\left( {{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}} \right)\) là số trung bình.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm: \({\Delta _Q} = {Q_3} - {Q_1}\).
a) Đúng. Số giờ nắng/ngày trung bình là:
\(\overline x = \frac{{1.5 + 2.4 + 3.2 + 4.7 + 5.12 + 6.0}}{{5 + 4 + 2 + 7 + 12}} = \frac{{107}}{{30}} \approx 3,57\).
b) Đúng. Khoảng biến thiên: R = 5,5 – 0,5 = 5.
c) Sai. Phương sai:
\({s^2} = \frac{1}{{30}}\left( {{{5.1}^2} + {{4.2}^2} + {{2.3}^2} + {{7.4}^2} + {{12.5}^2}} \right) - {\left( {\frac{{107}}{{30}}} \right)^2} = \frac{{2081}}{{900}} \approx 2,3\).
d) Đúng. \({Q_1} = 1,5 + \frac{{\frac{{30}}{4} - 5}}{4}.(2,5 - 1,5) = 2,125\).
\({Q_3} = 4,5 + \frac{{\frac{{3.30}}{4} - (5 + 4 + 2 + 7)}}{{12}}.(5,5 - 4,5) = 4,875\).
\({\Delta _Q} = {Q_3} - {Q_1} = 4,875 - 2,125 = 2,75\).
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 2\) cắt đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x + m\) tại 3 điểm phân biệt?
Lập phương trình hoành độ giao điểm của hai đồ thị hàm số.
Cô lập m, lập bảng biến thiên để xác định m sao cho hai đồ thị cắt nhau tại ba điểm phân biệt.
Phương trình hoành độ giao điểm là của hai đồ thị trên là:
\(2{x^3} - 3{x^2} + 2 = {x^3} - 6{x^2} + 9x + m \Leftrightarrow {x^3} + 3{x^2} - 9x + 2 = m\) (*)
Hai đồ thị cắt nhau tại 3 điểm phân biệt \( \Leftrightarrow \) (*) có 3 nghiệm phân biệt
\( \Leftrightarrow \) (C): \(y = {x^3} + 3{x^2} - 9x + 2\) cắt \(d:y = m\) tại 3 điểm phân biệt.
Xét (C): \(y = {x^3} + 3{x^2} - 9x + 2\).
Ta có \(y' = 3{x^2} + 6x - 9\); \(y' = 0 \Leftrightarrow x = - 3 \vee x = 1\).
Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy (C) cắt d tại 3 điểm phân biệt \( \Leftrightarrow - 3 < m < 29\).
Do m nguyên nên \(m \in \{ - 2; - 1;0;1;2;...,28\} \). Vậy có 31 giá trị của m thỏa mãn.
Một sân điền kinh gồm hai sân hình bán nguyệt có bán kính x (m, x > 0) và một sân hình chữ nhật như hình vẽ. Biết chu vi của sân điền kinh là 400 m, tìm diện tích lớn nhất của sân hình chữ nhật theo mét vuông (làm tròn kết quả đến hàng đơn vị).

Lập hàm số biểu diễn diện tích hình chữ nhật theo x.
Sử dụng đạo hàm tìm GTLN của hàm số.
Theo hình vẽ, một cạnh của hình chữ nhật có chiều dài 2x (m, x > 0).
Gọi độ dài cạnh còn lại là y (m, y > 0).
Chu vi sân là \(C = 2\pi x + 2y = 400\) (m).
Do đó \(y = \frac{{400 - 2\pi x}}{2} = 200 - \pi x\) (m).
Vì \(y > 0 \Leftrightarrow 200 - \pi x > 0 \Leftrightarrow x < \frac{{200}}{\pi }\).
Diện tích sân hình chữ nhật là:
\(S = 2xy = 2x(200 - x\pi ) = 400x - 2\pi {x^2}\) \(\left( {{m^2}} \right)\).
\(S' = 400 - 4\pi x = 0 \Leftrightarrow x = \frac{{100}}{\pi }\).
Ta có S(0) = 0, \(S\left( {\frac{{100}}{\pi }} \right) \approx 6366\), \(S\left( {\frac{{200}}{\pi }} \right) = 0\).
Vậy diện tích lớn nhất của hình chữ nhật là khoảng 6366 mét vuông.
Theo định luật II: Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật: $\overrightarrow{F} = m\overrightarrow{a}$, trong đó $\overrightarrow{F}$ là vecto lực (N), $\overrightarrow{a}$ là vector gia tốc $(m/s^2)$, m (kg) là khối lượng của vật. Muốn truyền cho quả bóng có khối lượng 0,5 (kg) một gia tốc 50 $(m/{{s}^{2}})$ thì cần một lực đá có độ lớn là bao nhiêu?

Thay số vào công thức đã cho.
Ta có: $\overrightarrow{F} = m\overrightarrow{a}$, suy ra $\left| {\overrightarrow{F}} \right|=\left| m\overrightarrow{a} \right|=m\left| {\overrightarrow{a}} \right|=0,5.50=25$.
Vậy muốn truyền cho quả bóng khối lượng 0,5 (kg) một gia tốc 50 thì cần một lực có độ lớn bằng 25 (N).
Hình dưới đây mô tả một sân cầu lông với kích thước theo tiêu chuẩn quốc tế. Ta chọn hệ trục Oxyz cho sân đó (đơn vị trên mỗi trục là mét) và hai điểm A, B như hình. Khi đó, tọa độ của , hãy tính: a + b + c (kết quả làm tròn đến hàng phần trăm).

Quan sát hình vẽ, xác định tọa độ các điểm A, B.
Ta có \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
Từ hình vẽ ta có A(6,7; 0; 0), B(6,7; 6,1; 1,55).
$\overrightarrow{AB}=(6,7-6,7;6,1-0;1,55-0)=(0;6,1;1,55)$.
$ \Rightarrow a + b + c = 0 + 6,1 + 1,55 = 7,65$.
• \(v\left( t \right) = h'\left( t \right)\).
• Xét hàm số \(h\left( t \right)\) trên đoạn \(\left[ {0;8} \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.
a) \(v\left( t \right) = h'\left( t \right) = {t^2} - 8t + 12\).
b) Xét hàm số \(h\left( t \right) = \frac{1}{3}{t^3} - 4{t^2} + 12t + 1\) trên đoạn \(\left[ {0;8} \right]\).
Ta có:
\(h'\left( t \right) = {t^2} - 8t + 12;h'\left( t \right) = 0 \Leftrightarrow t = 6\) hoặc \(t = 2\).
Bảng biến thiên:
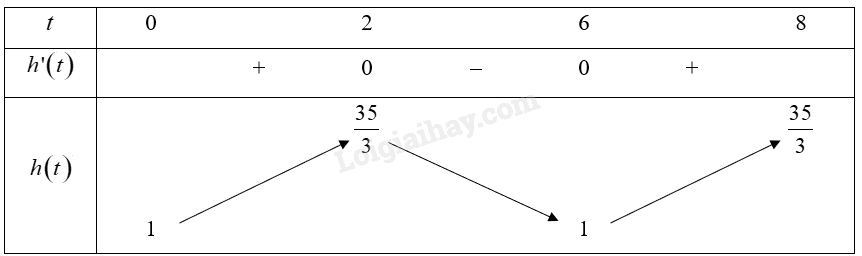
Vậy hàm số đồng biến trên các khoảng \(\left( {0;2} \right)\) và \(\left( {6;8} \right)\), hàm số nghịch biến trên khoảng \(\left( {2;6} \right)\).
Vậy chất điểm chuyển động lên trong khoảng thời gian từ 0 giây đến 2 giây và từ 6 giây đến 8 giây, chất điểm chuyển động đi xuống trong khoảng thời gian từ 2 giây đến 6 giây.
a) Tính \(\overrightarrow a - 2\overrightarrow b \) phụ thuộc tham số m sau đó giải từng điều kiện của tọa độ.
b) Tính \(\overrightarrow a \cdot \overrightarrow b \) theo tham số m sau đó giải theo điều kiện đề bài để tìm m.
c) Tính \(\left| {\overrightarrow a } \right|\) theo m sau đó giải theo điều kiện của đề để tìm m.
a) Ta có \(\overrightarrow a - 2\overrightarrow b = \left( {m - 2; - 1;0} \right)\). Để \(\overrightarrow a - 2\overrightarrow b = \left( {3; - 1;0} \right)\) thì \(\left\{ \begin{array}{l}m - 2 = 3\\ - 1 = - 1\\0 = 0\end{array} \right. \Leftrightarrow m = 5\).
b) Ta có \(\overrightarrow a \cdot \overrightarrow b = m + 6 + 18 = m + 24\). Để \(\overrightarrow a \cdot \overrightarrow b = 10\) thì \(m + 24 = 10 \Leftrightarrow m = - 14\)
c) Ta có \(\left| {\overrightarrow a } \right| = \sqrt {{m^2} + {3^3} + {6^2}} = \sqrt {{m^2} + 45} \).
Để \(\left| {\overrightarrow a } \right| = 9\) thì \(\sqrt {{m^2} + 45} = 9 \Leftrightarrow {m^2} + 45 = 81 \Leftrightarrow m = \pm 6\).
Tính giá trị đại diện
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

Cỡ mẫu: n = 100
Số trung bình: \(\overline x = \frac{{13.19,25 + 45.19,75 + 24.20,25 + 12.20,75 + 6.21,25}}{{100}} = 20,015\)
Phương sai: \({S^2} = \frac{{13.19,{{25}^2} + 45.19,{{75}^2} + 24.20,{{25}^2} + 12.20,{{75}^2} + 6.21,{{25}^2}}}{{100}} - 20,{015^2} \approx 0,28\)
Độ lệch chuẩn: \(\sigma = \sqrt {0,28} \approx 0,53\)
Đề thi học kì 1 Toán 12 - Đề số 9
Đề thi học kì 1 Toán 12 - Đề số 8
Đề thi học kì 1 Toán 12 - Đề số 7
Đề thi học kì 1 Toán 12 - Đề số 6
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số 1. Tính đơn điệu và cực trị của hàm số 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3. Đường tiệm cận của đồ thị hàm số 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn











Danh sách bình luận