Đề thi học kì 1 Toán 12 - Đề số 9
Đề thi học kì 1 Toán 12 - Đề số 9
Đề bài
Hàm số nào sau đây đồng biến trên $\mathbb{R}$?
-
A.
$y = x^{3} + 3x$.
-
B.
$y = x^{3} - 3x$.
-
C.
$y = \dfrac{x - 1}{x + 1}$.
-
D.
$y = x^{4} - 3x^{2} + 1$.
-
A.
M(-3; -3).
-
B.
x = -1.
-
C.
N(-1; 1).
-
D.
x = -3.
Cho hàm số $y = \frac{x-1}{2x+1}$. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\left[0; 2\right]$ lần lượt là $M$ và $m$. Mệnh đề nào sau đây đúng?
-
A.
$M + m = \frac{1}{5}$.
-
B.
$M + m = -\frac{1}{5}$.
-
C.
$M + m = -\frac{4}{5}$.
-
D.
$M + m = -1$.
Cho hàm số y = f(x) xác định trên ${\mathbb{R}}\backslash\left\{ 1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?

-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Cho hình lập phương ABCD. A’B’C’D’. Mệnh đề nào sau đây sai?
-
A.
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
-
B.
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
-
C.
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
-
D.
\(\overrightarrow {AB} = \overrightarrow {CD} \)
Gọi I là trung điểm của AB. Khẳng định nào sau đây sai?
-
A.
\(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \)
-
B.
\(IA = IB\)
-
C.
\(\overrightarrow {IA} = \overrightarrow {IB} \)
-
D.
\(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \)
Trong không gian Oxyz cho hai điểm $A\left( {\dfrac{1}{2}; - \dfrac{1}{3};5} \right)$, $B\left( {1;\dfrac{8}{3};\dfrac{3}{2}} \right)$. Tọa độ của vectơ $\overrightarrow{AB}$ là
-
A.
$\overset{\rightarrow}{AB}\left( {\dfrac{1}{2};3; - \dfrac{7}{2}} \right)$.
-
B.
$\overset{\rightarrow}{AB}\left( {\dfrac{3}{2};3; - \dfrac{7}{2}} \right)$.
-
C.
$\overset{\rightarrow}{AB}\left( {- \dfrac{1}{2}; - 3;\dfrac{7}{2}} \right)$.
-
D.
$\overset{\rightarrow}{AB}\left( {\dfrac{1}{2};\dfrac{8}{3}; - \dfrac{7}{2}} \right)$.
Trong không gian Oxyz, cosin của góc giữa hai vecto \(\overrightarrow u = (10;10;20)\), \(\overrightarrow v = (10; - 20;10)\) là
-
A.
\(\frac{1}{6}\)
-
B.
\(\frac{1}{2}\)
-
C.
\( - \frac{1}{6}\)
-
D.
\( - \frac{1}{2}\)
Trong không gian (Oxyz), cho \(\Delta ABC\) có \(\overrightarrow {AB} = (4; - 1; - 5)\), \(\overrightarrow {BC} = (2; - 4; - 2)\), gọi M là trung điểm BC. Độ dài đoạn AM là
-
A.
\(\sqrt {70} \)
-
B.
\(2\sqrt {70} \)
-
C.
\(\sqrt 6 \)
-
D.
\(\frac{{\sqrt {110} }}{2}\)
Trong không gian Oxyz, cho tam giác ABC với A(1;3;4), B(2;−1;0), C(3;1;2). Tọa độ trọng tâm G của tam giác ABC là
-
A.
\(G\left( {3;\frac{3}{2};3} \right)\)
-
B.
\(G\left( {2; - 1;2} \right)\)
-
C.
\(G\left( {2;1;2} \right)\)
-
D.
\(G\left( {6;3;6} \right)\)
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:

Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là
-
A.
$R = 4$.
-
B.
$R = 20$.
-
C.
$R = 9$.
-
D.
$R = 108$.
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khoẻ. Qua thống kê quãng đường 20 ngày đi bộ (đơn vị: km) của bác Hương tính được độ lệch chuẩn của mẫu số liệu ghép nhóm là 6. Phương sai của mẫu số liệu trên là
-
A.
12.
-
B.
2,45.
-
C.
36.
-
D.
13.
Một ngôi nhà gồm hai phần: phần thân nhà dạng hình hộp chữ nhật $ABCD.OMNK$có chiều dài $1200\mspace{6mu} cm$, chiều rộng $900\mspace{6mu} cm$, chiều cao $450\mspace{6mu} cm$, phần mái nhà dạng hình chóp $S.ABCD$ có các cạnh bên bằng nhau và cùng tạo với mặt đáy một góc $\alpha$ có $\tan\alpha = \dfrac{1}{5}$. Chọn hệ trục toạ độ $Oxyz$ có mỗi vectơ đơn vị trên mỗi trục có độ dài $1\mspace{6mu} cm$ sao cho $M$ thuộc tia $Ox$, $K$ thuộc tia $Oy$, $A$ thuộc tia $Oz$ (như hình vẽ).
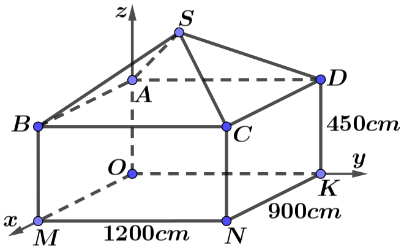
Các mệnh đề sau đúng hay sai?
a) Tọa độ điểm $B\left( {900;1200;450} \right)$.
b) $\alpha = \widehat{SAC}$.
c) $SA = 150\mspace{6mu} cm$.
d) Biết $S\left( {a;b;c} \right)$ thì giá trị của biểu thức $P = a + b + c = 1500$.
Một huấn luyện viên môn bóng rổ thống kê lại số quả bóng được ném vào rổ của một nhóm vận động viên đang tập luyện mỗi người ném 11 lần như sau:
a) Từ biểu đồ, có thể lập được bảng tần số ghép nhóm gồm 5 nhóm biết mỗi nhóm có độ dài là 2.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lớn hơn 5.
c) Số trung bình của mẫu số liệu bằng \(\frac{{85}}{{14}}\).
d) Độ lệch chuẩn của mẫu số liệu trên lớn hơn 3.
Xí nghiệp \( A \) sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \( TC = x^3 - 77x^2 + 1000x + 4000 \) và hàm doanh thu là \( TR = -2x^2 + 1312x \), với \( x \) là số sản phẩm. Lợi nhuận của xí nghiệp \( A \) được xác định bằng hàm số \( f(x) = TR - TC \), cực đại lợi nhuận của xí nghiệp \( A \) khi đó đạt bao nhiêu sản phẩm?
Sự ảnh hưởng khi sử dụng một loại độc tố với vi khuẩn X được một nhà sinh học mô tả bởi hàm số \(P(t) = \frac{{t + 1}}{{{t^2} + t + 4}}\), trong đó P(t) là số lượng vi khuẩn sau t giờ sử dụng độc tố. Hỏi sau bao nhiêu giờ thì số lượng vi khuẩn X bắt đầu giảm?
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = ( - 4;2;5)\) và \(\overrightarrow b = (3m + 2;2;6 - n)\). Tính giá trị biểu thức \(6m + 2n\) để hai vecto \(\overrightarrow a \), \(\overrightarrow b \) bằng nhau.
Trạm kiểm soát không lưu đang theo dõi hai máy bay. Giả sử trong không gian với hệ trục tọa độ Oxyz, đơn vị đo lấy theo kilômét, tại cùng một thời điểm theo dõi ban đầu: máy bay thứ nhất ở tọa độ A(0;35;10), bay theo hướng vectơ \(\overrightarrow {{v_1}}= \left( {3;4;0} \right)\) với tốc độ không đổi 900(km/h) và máy bay thứ hai ở tọa độ B(31;10;11), bay theo hướng \(\overrightarrow {{v_2}} = \left( {5;12;0} \right)\) với tốc độ không đổi 910 (km/h). Biết rằng khoảng cách an toàn tối thiểu giữa hai máy bay là 5 hải lý (khoảng 9,3 km). Nếu hai máy bay tiếp tục duy trì hướng và tốc độ bay như trên thì sau ít nhất bao nhiêu phút (kể từ thời điểm theo dõi ban đầu), hai máy bay vi phạm khoảng cách an toàn (kết quả làm tròn đến hàng phần trăm)?
Lời giải và đáp án
Hàm số nào sau đây đồng biến trên $\mathbb{R}$?
-
A.
$y = x^{3} + 3x$.
-
B.
$y = x^{3} - 3x$.
-
C.
$y = \dfrac{x - 1}{x + 1}$.
-
D.
$y = x^{4} - 3x^{2} + 1$.
Đáp án : A
Cho hàm số y = f(x) liên tục trên K.
- Nếu f’(x) dương thì hàm số y = f(x) đồng biến trên K.
- Nếu f’(x) âm thì hàm số y = f(x) nghịch biến trên K.
Ta có với \(y = {x^3} + 3x\) thì \(y' = 3{x^2} + 3 > 0\), \(\forall x\).
-
A.
M(-3; -3).
-
B.
x = -1.
-
C.
N(-1; 1).
-
D.
x = -3.
Đáp án : A
Cho đồ thị hàm số y = f(x).
Tại điểm mà đồ thị đổi hướng:
- Lên \( \to \) xuống (trái sang phải): cực đại.
- Xuống \( \to \) lên (trái sang phải): cực tiểu.
Dựa vào đồ thị, ta thấy điểm M(-3; -3) là điểm cực đại của đồ thị hàm số đã cho.
Cho hàm số $y = \frac{x-1}{2x+1}$. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\left[0; 2\right]$ lần lượt là $M$ và $m$. Mệnh đề nào sau đây đúng?
-
A.
$M + m = \frac{1}{5}$.
-
B.
$M + m = -\frac{1}{5}$.
-
C.
$M + m = -\frac{4}{5}$.
-
D.
$M + m = -1$.
Đáp án : C
Tính đạo hàm để xét sự biến thiên của hàm số, từ đó tìm GTLN và GTNN trên [0;2].
\(y' = \frac{3}{{{{(2x + 1)}^2}}} > 0\) \(\forall x \ne - \frac{1}{2}\).
Hàm số đồng biến trên [0;2], do đó hàm đạt GTNN tại x = 0, đạt GTLN tại x = 2.
\(M = f(0) = - 1\); \(m = f(2) = \frac{1}{5}\).
Vậy \(M + m = - 1 + \frac{1}{5} = - \frac{4}{5}\).
Cho hàm số y = f(x) xác định trên ${\mathbb{R}}\backslash\left\{ 1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?

-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Đáp án : C
Cho hàm số $y = f(x)$.
Đường thẳng $y = y_{0}$ là TCN của đồ thị hàm số nếu thỏa mãn một trong những điều kiện sau:
$\lim\limits_{x\rightarrow + \infty}y = y_{0}$ hoặc $\lim\limits_{x\rightarrow - \infty}y = y_{0}$.
Đường thằng $x = x_{0}$ là TCĐ của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau:
$\lim\limits_{x\rightarrow x_{0} +}y = + \infty$ hoặc $\lim\limits_{x\rightarrow x_{0} +}y = - \infty$ hoặc $\lim\limits_{x\rightarrow x_{0} -}y = + \infty$ hoặc $\lim\limits_{x\rightarrow x_{0} -}y = - \infty$.
Đồ thị hàm số có
\(\mathop {\lim }\limits_{x \to + \infty } y = 2\), \(\mathop {\lim }\limits_{x \to - \infty } y = - 3\) và \(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \), \(\mathop {\lim }\limits_{x \to {1^ - }} = - \infty \)
nên có 1 đường tiệm cận đứng là x = 1 và hai đường tiệm cận ngang là y = -3; y = 2.
Cho hình lập phương ABCD. A’B’C’D’. Mệnh đề nào sau đây sai?
-
A.
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
-
B.
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
-
C.
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
-
D.
\(\overrightarrow {AB} = \overrightarrow {CD} \)
Đáp án : D
Xét từng đáp án, sử dụng phương pháp loại trừ.
Áp dụng các quy tắc vecto: quy tắc hình bình hành, quy tắc hình hộp, khái niệm vecto bằng nhau, độ dài vecto.
Đáp án A đúng theo quy tắc hình hộp.
Đáp án B đúng theo quy tắc hình bình hành.
Đáp án C đúng vì \(\left| {\overrightarrow {AB} } \right| = AB = CD = \left| {\overrightarrow {CD} } \right|\).
Đáp án D sai vì \(\overrightarrow {AB} \), \(\overrightarrow {CD} \) là hai vecto ngược hướng nên chúng không bằng nhau.
Gọi I là trung điểm của AB. Khẳng định nào sau đây sai?
-
A.
\(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \)
-
B.
\(IA = IB\)
-
C.
\(\overrightarrow {IA} = \overrightarrow {IB} \)
-
D.
\(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \)
Đáp án : C
Sử dụng tính chất trung điểm.
C sai vì \(\overrightarrow {IA} = - \overrightarrow {IB} \) do hai vecto này ngược hướng.
Trong không gian Oxyz cho hai điểm $A\left( {\dfrac{1}{2}; - \dfrac{1}{3};5} \right)$, $B\left( {1;\dfrac{8}{3};\dfrac{3}{2}} \right)$. Tọa độ của vectơ $\overrightarrow{AB}$ là
-
A.
$\overset{\rightarrow}{AB}\left( {\dfrac{1}{2};3; - \dfrac{7}{2}} \right)$.
-
B.
$\overset{\rightarrow}{AB}\left( {\dfrac{3}{2};3; - \dfrac{7}{2}} \right)$.
-
C.
$\overset{\rightarrow}{AB}\left( {- \dfrac{1}{2}; - 3;\dfrac{7}{2}} \right)$.
-
D.
$\overset{\rightarrow}{AB}\left( {\dfrac{1}{2};\dfrac{8}{3}; - \dfrac{7}{2}} \right)$.
Đáp án : A
Với hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\), ta có \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
\(\overrightarrow {AB} = \left( {1 - \frac{1}{2};\frac{8}{3} + \frac{1}{3};\frac{3}{2} - 5} \right) = \left( {\frac{1}{2};3; - \frac{7}{2}} \right)\).
Trong không gian Oxyz, cosin của góc giữa hai vecto \(\overrightarrow u = (10;10;20)\), \(\overrightarrow v = (10; - 20;10)\) là
-
A.
\(\frac{1}{6}\)
-
B.
\(\frac{1}{2}\)
-
C.
\( - \frac{1}{6}\)
-
D.
\( - \frac{1}{2}\)
Đáp án : A
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}\).
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{10.10 + 10.( - 20) + 20.10}}{{\sqrt {{{10}^2} + {{10}^2} + {{20}^2}} .\sqrt {{{10}^2} + {{( - 20)}^2} + {{10}^2}} }} = \frac{1}{6}\).
Trong không gian (Oxyz), cho \(\Delta ABC\) có \(\overrightarrow {AB} = (4; - 1; - 5)\), \(\overrightarrow {BC} = (2; - 4; - 2)\), gọi M là trung điểm BC. Độ dài đoạn AM là
-
A.
\(\sqrt {70} \)
-
B.
\(2\sqrt {70} \)
-
C.
\(\sqrt 6 \)
-
D.
\(\frac{{\sqrt {110} }}{2}\)
Đáp án : A
Áp dụng quy tắc ba điểm tính \(\overrightarrow {AC} \), quy tắc trung điểm tính \(\overrightarrow {AM} \). Từ đó, tìm độ dài AM.
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} = (4 + 2; - 1 - 4; - 5 - 2) = (6; - 5; - 7)\); \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{2}\left( {4 + 6; - 1 - 5; - 5 - 7} \right) = \left( {5; - 3; - 6} \right)\).
Suy ra \(AM = \sqrt {{5^2} + {{( - 3)}^2} + {{( - 6)}^2}} = \sqrt {70} \).
Trong không gian Oxyz, cho tam giác ABC với A(1;3;4), B(2;−1;0), C(3;1;2). Tọa độ trọng tâm G của tam giác ABC là
-
A.
\(G\left( {3;\frac{3}{2};3} \right)\)
-
B.
\(G\left( {2; - 1;2} \right)\)
-
C.
\(G\left( {2;1;2} \right)\)
-
D.
\(G\left( {6;3;6} \right)\)
Đáp án : C
Với G là trọng tâm tam giác ABC, ta có \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3}\end{array} \right.\).
\(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 2 + 3}}{3} = 2\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + ( - 1) + 1}}{2} = 1\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{4 + 0 + 2}}{3} = 2\end{array} \right. \Rightarrow G(2;1;2)\).
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:

Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là
-
A.
$R = 4$.
-
B.
$R = 20$.
-
C.
$R = 9$.
-
D.
$R = 108$.
Đáp án : B
Để tính khoảng biến thiên, ta lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên (nhóm chứa mẫu số liệu).
Khoảng biến thiên: R = 30 - 10 = 20.
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khoẻ. Qua thống kê quãng đường 20 ngày đi bộ (đơn vị: km) của bác Hương tính được độ lệch chuẩn của mẫu số liệu ghép nhóm là 6. Phương sai của mẫu số liệu trên là
-
A.
12.
-
B.
2,45.
-
C.
36.
-
D.
13.
Đáp án : C
Phương sai bằng bình phương độ lệch chuẩn.
Phương sai của mẫu số liệu trên là \(6^2 = 36\).
Một ngôi nhà gồm hai phần: phần thân nhà dạng hình hộp chữ nhật $ABCD.OMNK$có chiều dài $1200\mspace{6mu} cm$, chiều rộng $900\mspace{6mu} cm$, chiều cao $450\mspace{6mu} cm$, phần mái nhà dạng hình chóp $S.ABCD$ có các cạnh bên bằng nhau và cùng tạo với mặt đáy một góc $\alpha$ có $\tan\alpha = \dfrac{1}{5}$. Chọn hệ trục toạ độ $Oxyz$ có mỗi vectơ đơn vị trên mỗi trục có độ dài $1\mspace{6mu} cm$ sao cho $M$ thuộc tia $Ox$, $K$ thuộc tia $Oy$, $A$ thuộc tia $Oz$ (như hình vẽ).

Các mệnh đề sau đúng hay sai?
a) Tọa độ điểm $B\left( {900;1200;450} \right)$.
b) $\alpha = \widehat{SAC}$.
c) $SA = 150\mspace{6mu} cm$.
d) Biết $S\left( {a;b;c} \right)$ thì giá trị của biểu thức $P = a + b + c = 1500$.
a) Tọa độ điểm $B\left( {900;1200;450} \right)$.
b) $\alpha = \widehat{SAC}$.
c) $SA = 150\mspace{6mu} cm$.
d) Biết $S\left( {a;b;c} \right)$ thì giá trị của biểu thức $P = a + b + c = 1500$.
Áp dụng biểu thức tọa độ các phép toán vecto.
a) Sai. Tọa độ điểm \(B\left( {900;0;450} \right)\) nên mệnh đề sai.
b) Đúng. Gọi \(I\) là giao điểm của \(AC\) và \(BD\), do hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và \(ABCD\) là hình chữ nhật nên \(SI \bot (ABCD)\). Do đó \(\left( {SA,(ABCD)} \right) = \left( {SA,IA} \right) = \widehat {SAI} = \widehat {SAC}\).
Vậy mệnh đề đúng.
c) Sai. Ta có \(IA = \frac{1}{2}\sqrt {A{B^2} + B{C^2}} = 750\;cm\) và \(\frac{1}{{{{\cos }^2}\alpha }} = 1 + {\tan ^2}\alpha \Rightarrow \cos \alpha = \frac{5}{{\sqrt {26} }}\)
Do đó \(SA = \frac{{IA}}{{\cos \alpha }} = 150\sqrt {26} \;cm\).
Vậy mệnh đề sai.
d) Sai. Ta có \(A\left( {0;0;450} \right),\;C\left( {900;1200;450} \right) \Rightarrow I\left( {450;600;450} \right)\).
Mà \(SI = IA\tan \alpha = 150\) nên \(S\left( {450;600;600} \right)\).
Vậy \(P = 450 + 600 + 600 = 1650\) nên mệnh đề sai.
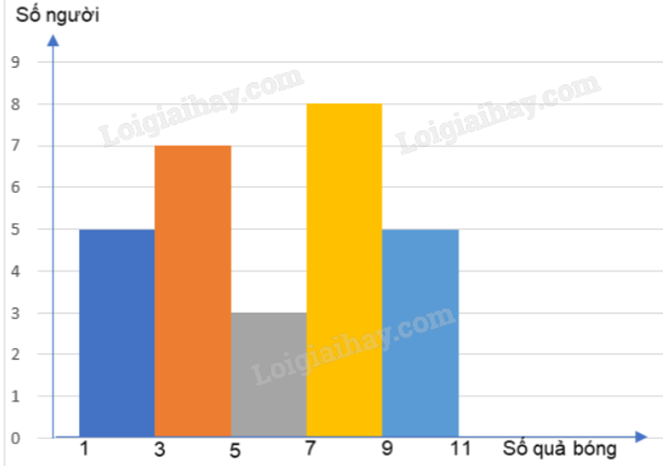
Một huấn luyện viên môn bóng rổ thống kê lại số quả bóng được ném vào rổ của một nhóm vận động viên đang tập luyện mỗi người ném 11 lần như sau:

a) Từ biểu đồ, có thể lập được bảng tần số ghép nhóm gồm 5 nhóm biết mỗi nhóm có độ dài là 2.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lớn hơn 5.
c) Số trung bình của mẫu số liệu bằng \(\frac{{85}}{{14}}\).
d) Độ lệch chuẩn của mẫu số liệu trên lớn hơn 3.
a) Từ biểu đồ, có thể lập được bảng tần số ghép nhóm gồm 5 nhóm biết mỗi nhóm có độ dài là 2.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lớn hơn 5.
c) Số trung bình của mẫu số liệu bằng \(\frac{{85}}{{14}}\).
d) Độ lệch chuẩn của mẫu số liệu trên lớn hơn 3.
Lập bảng tần số ghép nhóm, áp dụng công thức tính khoảng tứ phân vị, số trung bình và độ lệch chuẩn.
a) Đúng. Bảng tần số ghép nhóm thoả mãn yêu cầu:

Vậy có 5 nhóm, mỗi nhóm có độ dài bằng 2.
b) Sai. Gọi \({x_1},{x_2},...,{x_{{x_{28}}}}\) lần lượt là số quả bóng được ném vào rổ của các vận động viên sắp xếp theo thứ tự
không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_7} + {x_8}} \right) \in \left[ {3;5} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu
ghép nhóm là \({Q_1} = 3 + \frac{{\frac{{28}}{4} - 5}}{7}\left( {5 - 3} \right) = \frac{{25}}{7}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right) \in \left[ {7;9} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \({Q_1} = 7 + \frac{{\frac{{3.28}}{4} - 15}}{8}\left( {9 - 7} \right) = \frac{{17}}{2}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{17}}{2} - \frac{{25}}{7} \approx 4,93\).
c) Đúng. Ta có bảng thống kê theo giá trị đại diện:
Cỡ mẫu: n = 28.
Số trung bình của mẫu số liệu: \(\overline x = \frac{1}{{28}}\left( {5.2 + 7.4 + 3.6 + 8.8 + 5.10} \right) = \frac{{85}}{{14}}\).
d) Sai. Phương sai của mẫu số liệu:
\({S^2} = \frac{1}{{28}}\left( {{{5.2}^2} + {{7.4}^2} + {{3.6}^2} + {{8.8}^2} + {{5.10}^2}} \right) - {\left( {\frac{{85}}{{14}}} \right)^2} = \frac{{1539}}{{196}}\).
Độ lệch chuẩn của mẫu số liệu trên là: \(S = \sqrt {\frac{{1539}}{{196}}} \approx 2,802\).
Xí nghiệp \( A \) sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \( TC = x^3 - 77x^2 + 1000x + 4000 \) và hàm doanh thu là \( TR = -2x^2 + 1312x \), với \( x \) là số sản phẩm. Lợi nhuận của xí nghiệp \( A \) được xác định bằng hàm số \( f(x) = TR - TC \), cực đại lợi nhuận của xí nghiệp \( A \) khi đó đạt bao nhiêu sản phẩm?
Xét hàm \( f(x) = TR - TC \): Tính đạo hàm, lập bảng biến thiên để tìm cực đại của hàm số.
\( f(x) = TR - TC = -2x^2 + 1312x - \left( x^3 - 77x^2 + 1000x + 4000 \right) \)
\( = -x^3 + 75x^2 + 312x - 4000 \).
TXĐ: \( D = (0; +\infty) \).
Ta có
\(f'(x) = - 3{x^2} + 150x + 312 = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 52}\\{x = - 2}\end{array}\begin{array}{*{20}{c}}{}\\{}\end{array}} \right.\begin{array}{*{20}{c}}{(L)}\\{(TM)}\end{array}\)
Bảng biến thiên:
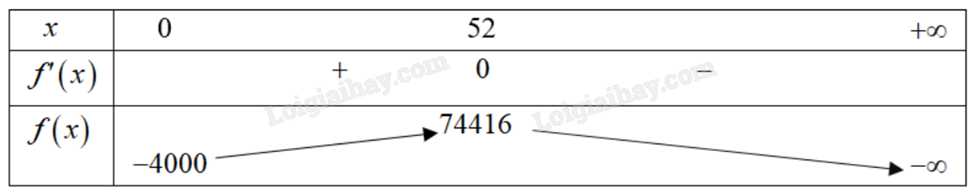
Vậy lợi nhuận của công ty đạt cực đại khi số sản phẩm bằng 52.
Sự ảnh hưởng khi sử dụng một loại độc tố với vi khuẩn X được một nhà sinh học mô tả bởi hàm số \(P(t) = \frac{{t + 1}}{{{t^2} + t + 4}}\), trong đó P(t) là số lượng vi khuẩn sau t giờ sử dụng độc tố. Hỏi sau bao nhiêu giờ thì số lượng vi khuẩn X bắt đầu giảm?
Lập bảng biến thiên của hàm số P(t) và tìm thời điểm mà qua đó P’(t) mang dấu âm.
Xét hàm số \(P(t) = \frac{{t + 1}}{{{t^2} + t + 4}}\) với \(t \ge 0\).
Ta có \(P'(t) = \frac{{{t^2} + t + 4 - (t + 1)(2t + 1)}}{{{{({t^2} + t + 4)}^2}}} = \frac{{ - {t^2} - 2t + 3}}{{{{({t^2} + t + 4)}^2}}}\).
\(P'(t) = 0 \Leftrightarrow - {t^2} - 2t + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\,\,(TM)\\t = - 3\,\,(L)\end{array} \right.\)
Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy sau 1 giờ thì số lượng vi khuẩn X bắt đầu giảm.
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = ( - 4;2;5)\) và \(\overrightarrow b = (3m + 2;2;6 - n)\). Tính giá trị biểu thức \(6m + 2n\) để hai vecto \(\overrightarrow a \), \(\overrightarrow b \) bằng nhau.
Hai vecto bằng nhau: Nếu cho \(\overrightarrow a = (x;y)\) và \(\overrightarrow b = (x';y')\) thì \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = x'}\\{y = y'}\end{array}} \right.\).
\(\overrightarrow a = \overrightarrow b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{3m + 2 = - 4}\\{2 = 2}\\{6 - n = 5}\end{array}} \right. \)
\(\Rightarrow \left\{ {\begin{array}{*{20}{l}}{m = - 2}\\{n = 1}\end{array}} \right. \Rightarrow 6m + 2n = 6.( - 2) + 2.1 = - 10.\)
Trạm kiểm soát không lưu đang theo dõi hai máy bay. Giả sử trong không gian với hệ trục tọa độ Oxyz, đơn vị đo lấy theo kilômét, tại cùng một thời điểm theo dõi ban đầu: máy bay thứ nhất ở tọa độ A(0;35;10), bay theo hướng vectơ \(\overrightarrow {{v_1}}= \left( {3;4;0} \right)\) với tốc độ không đổi 900(km/h) và máy bay thứ hai ở tọa độ B(31;10;11), bay theo hướng \(\overrightarrow {{v_2}} = \left( {5;12;0} \right)\) với tốc độ không đổi 910 (km/h). Biết rằng khoảng cách an toàn tối thiểu giữa hai máy bay là 5 hải lý (khoảng 9,3 km). Nếu hai máy bay tiếp tục duy trì hướng và tốc độ bay như trên thì sau ít nhất bao nhiêu phút (kể từ thời điểm theo dõi ban đầu), hai máy bay vi phạm khoảng cách an toàn (kết quả làm tròn đến hàng phần trăm)?
Tìm tọa độ hai máy bay sau t giờ sau đó lập phương trình khoảng cách tối thiểu.
Đặt \(A'\left( {3a;4a + 35;10} \right)\) là điểm di chuyển của máy bay thứ nhất.
Gọi t (giờ) là thời điểm mà hai máy bay bay sau t giờ vi phạm khoảng cách an toàn.
Ta có khoảng cách so với điểm ban đầu là \(A'A = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 900t \Leftrightarrow a = 180t\).
\( \Rightarrow A'\left( {540t;35 + 720t;10} \right)\).
Tương tự ta đặt điểm \(B'\left( {5b + 31;12b + 10;11} \right)\) là điểm di chuyển của máy bay thứ hai.
Khi đó \(\sqrt {{{\left( {5b} \right)}^2} + {{\left( {12b} \right)}^2}} = 910t \Rightarrow b = 70t\) suy ra \(B\left( {31 + 350t;10 + 840t;11} \right)\).
Vì khoảng cách tối thiếu để hai máy bay an toàn là 9,3 km và hai máy bay vi phạm khoảng cách an toàn nên:
\(A'B' \le 9,3 \Leftrightarrow {\left( {31 - 190t} \right)^2} + {\left( { - 25 + 120t} \right)^2} + {\left( 1 \right)^2} \le 9,{3^2}\)
\( \Leftrightarrow 0,1403 \le t \le 0,21177\) (giờ).
Vậy sau ít nhất 0,1403 giờ hay 8,42 phút thì vi phạm khoảng cách an toàn.
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
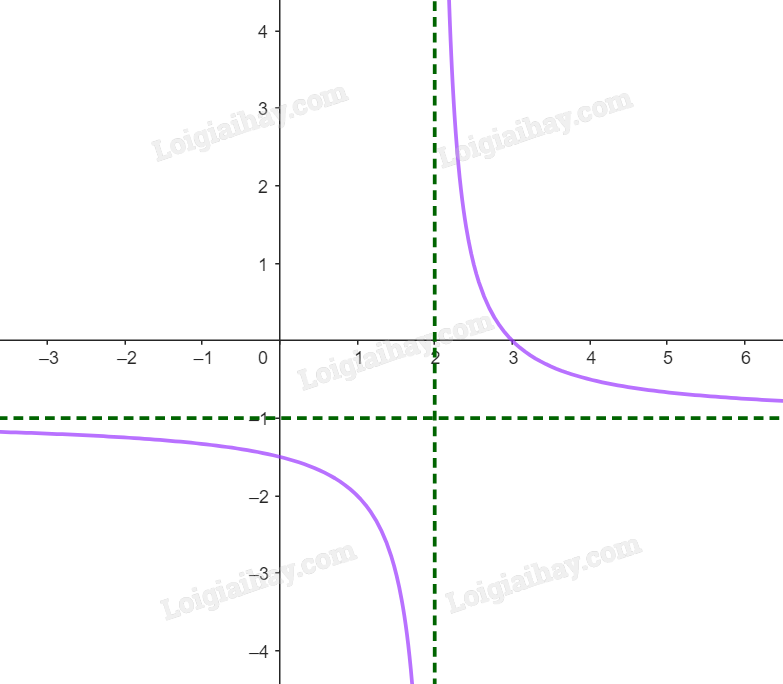
1) TXĐ: \(D = \mathbb{R}\backslash \{ 2\} \).
2) Sự biến thiên:
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty \); \(\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \). Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = - 1\); \(\mathop {\lim }\limits_{x \to - \infty } y = - 1\). Do đó, đường thẳng y = -1 là tiệm cận ngang của đồ thị hàm số.
Đạo hàm: \(y' = \frac{{ - 1}}{{{{( - x + 2)}^2}}} > 0\), với mọi \(x \ne 2\).
Bảng biến thiên:
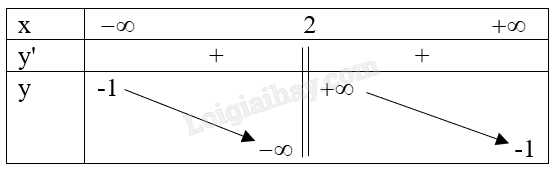
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\), \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
3) Đồ thị:
- Giao điểm của đồ thị với trục tung: \(\left( {0; - \frac{3}{2}} \right)\).
- Giao điểm của đồ thị với trục hoành: (3;0).
- Đồ thị hàm số đi qua các điểm \(\left( {0; - \frac{3}{2}} \right)\), (-3;0), (1;-2) và \(\left( {\frac{5}{2};1} \right)\).
- Đồ thị hàm số nhận giao điểm (2;-1) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Ta vẽ được đồ thị \(y = \frac{{x - 3}}{{ - x + 2}}\) như hình:
\(H\) là chân đường cao hạ từ \(A\) xuống \(BC\) thì ta tìm điểm \(H\) sao cho \(\left\{ \begin{array}{l}AH \bot BC\\H \in BC\end{array} \right.\).
Giả sử \(H\left( {x;y;z} \right)\). Ta có
\(\overrightarrow {AH} = \left( {x;y;z - 1} \right),\overrightarrow {BC} = \left( {3;3; - 1} \right)\)
Vì \(H\) là chân đường cao hạ từ \(A\) xuống \(BC\) nên \(AH \bot BC\)
\( \Rightarrow \overrightarrow {AH} .\overrightarrow {BC} = 0 \Rightarrow x.3 + y.3 + \left( {z - 1} \right).\left( { - 1} \right) = 0 \Leftrightarrow 3{\rm{x}} + 3y - z = - 1\left( 1 \right)\)
\(\overrightarrow {BH} = \left( {x + 1;y + 2;z} \right)\)
Vì \(H \in BC\) nên hai vectơ \(\overrightarrow {BH} ,\overrightarrow {BC} \) cùng phương.
\( \Leftrightarrow \frac{{x + 1}}{3} = \frac{{y + 2}}{3} = \frac{z}{{ - 1}} \Leftrightarrow \left\{ \begin{array}{l}\frac{{x + 1}}{3} = \frac{{y + 2}}{3}\\\frac{{x + 1}}{3} = \frac{z}{{ - 1}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 1 = y + 2\\ - \left( {x + 1} \right) = 3{\rm{z}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 1\left( 2 \right)\\x + 3{\rm{z}} = - 1\left( 3 \right)\end{array} \right.\)
Từ (1), (2), (3) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}3{\rm{x}} + 3y - z = - 1\\x - y = 1\\x + 3{\rm{z}} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{{19}}\\y = - \frac{{14}}{{19}}\\z = - \frac{8}{{19}}\end{array} \right.\)
Vậy \(H\left( {\frac{5}{{19}}; - \frac{{14}}{{19}}; - \frac{8}{{19}}} \right)\).
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Sử dụng kiến thức về ý nghĩa của độ lệch chuẩn để nhận xét: Độ lệch chuẩn dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Ta có bảng số liệu với giá trị đại diện:

Phân xưởng 1: Tổng số linh kiện: \(4 + 9 + 13 + 8 + 6 = 40\)
Giá trị trung bình \(\overline {{x_1}} = \frac{{1,75.4 + 2,25.9 + 2,75.13 + 3,25.8 + 3,75.6}}{{4 + 9 + 13 + 8 + 6}} = \frac{{223}}{{80}}\)
Phương sai: \(s_1^2 = \frac{1}{{40}}\left( {1,{{75}^2}.4 + 2,{{25}^2}.9 + 2,{{75}^2}.13 + 3,{{25}^2}.8 + 3,{{75}^2}.6} \right) - {\left( {\frac{{223}}{{80}}} \right)^2} = \frac{{2271}}{{6400}}\)
Độ lệch chuẩn: \({s_1} = \sqrt {\frac{{2271}}{{6400}}} \approx 0,6\)
Phân xưởng 2: Tổng số linh kiện: \(2 + 8 + 20 + 7 + 3 = 40\)
Giá trị trung bình \(\overline {{x_2}} = \frac{{1,75.2 + 2,25.8 + 2,75.20 + 3,25.7 + 3,75.3}}{{2 + 8 + 20 + 7 + 3}} = \frac{{221}}{{80}}\)
Phương sai: \(s_2^2 = \frac{1}{{40}}\left( {1,{{75}^2}.2 + 2,{{25}^2}.8 + 2,{{75}^2}.20 + 3,{{25}^2}.7 + 3,{{75}^2}.3} \right) - {\left( {\frac{{221}}{{80}}} \right)^2} = \frac{{1399}}{{6400}}\)
Độ lệch chuẩn: \({s_2} = \sqrt {\frac{{1399}}{{6400}}} \approx 0,47\)
Vì \(0,6 > 0,47\) nên độ phân tán của phân xưởng 1 lớn hơn độ phân tán của phân xưởng 2.
Đề thi học kì 1 Toán 12 - Đề số 10
Đề thi học kì 1 Toán 12 - Đề số 8
Đề thi học kì 1 Toán 12 - Đề số 7
Đề thi học kì 1 Toán 12 - Đề số 6
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số 1. Tính đơn điệu và cực trị của hàm số 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3. Đường tiệm cận của đồ thị hàm số 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn












Danh sách bình luận