Đề thi học kì 1 Toán 12 - Đề số 8
Đề thi học kì 1 Toán 12 - Đề số 8
Đề bài
Cho hàm số y = f(x) có đồ thị như hình vẽ.

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
$(-\infty; 2)$.
-
B.
(1; 3).
-
C.
(0; 3).
-
D.
(0; 2).
Hàm số $y = x^3 - 3x - 2025$ nghịch biến trên khoảng nào dưới đây?
-
A.
$\left(-1; 1\right)$.
-
B.
$\left(0; 3\right)$.
-
C.
$\left(-\infty; -1\right)$.
-
D.
$\left(1; 3\right)$.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x^{4} - 2x^{2} - 1$ trên đoạn $\left\lbrack {- 1;2} \right\rbrack$. Giá trị của biểu thức M + 3m bằng
-
A.
1.
-
B.
5.
-
C.
6.
-
D.
4.
-
A.
$y = \dfrac{x^{2} - x - 1}{x - 2}$.
-
B.
$y = \dfrac{x^{2} - x + 1}{x + 2}$.
-
C.
$y = \dfrac{x^{2} - 2x - 1}{x - 2}$.
-
D.
$y = \dfrac{- x^{2} + x - 1}{x - 2}$.
Cho hình lập phương ABCD.A’B’C’D’. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
-
A.
\(\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
B.
\(\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
C.
\(\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
D.
\(\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
Trong không gian Oxyz, O là gốc tọa độ, $\overrightarrow{OM} = - \overrightarrow{i} - 2\overrightarrow{k}$. Tọa độ của điểm M là
-
A.
(1; 0; -2).
-
B.
(1; 0; 2).
-
C.
(-1; -2; 0).
-
D.
(-1; 0; -2).
Trong không gian Oxyz, cho hai điểm A(3;-2;1) và B(4;2;3). Vecto $\overrightarrow{AB}$ có tọa độ là:
-
A.
(-1;0;2).
-
B.
(1;4;2).
-
C.
(1;0;2).
-
D.
(-1;-4;-2).
Cho \(\overrightarrow {AB} = \left( {1;3;2} \right)\). Tọa độ của \(\overrightarrow a = 2\overrightarrow {AB} \) là
-
A.
\(\left( {2;6;4} \right)\)
-
B.
\(\left( {2;3;4} \right)\)
-
C.
\(\left( {2;6;2} \right)\)
-
D.
\(\left( {1;6;4} \right)\)
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (1; - 2;1)\) và \(\overrightarrow b = (2; - 4; - 2)\). Khi đó \(\overrightarrow a .\overrightarrow b \) bằng
-
A.
8
-
B.
-8
-
C.
12
-
D.
-12
Trong không gian Oxy, cho điểm A(-5;2;3) và B là điểm đối xứng với A qua trục Oy. Độ dài đoạn thẳng AB bằng
-
A.
\(\sqrt {34} \)
-
B.
\(\sqrt 8 \)
-
C.
\(2\sqrt {34} \)
-
D.
\(\sqrt {38} \)
Chiều cao của 40 học sinh lớp 12A được ghi lại như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng:
-
A.
30.
-
B.
5.
-
C.
25.
-
D.
20.
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 30 con hồ và thu được kết quả như sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là:
-
A.
1,38.
-
B.
1,27.
-
C.
2,3.
-
D.
1,71.
Trong không gian $Oxyz$ cho các điểm $A\left( {5;1;3} \right);\, B\left( {4;2;3} \right);\, C\left( {5;0;3} \right)$.
a) $\overset{\rightarrow}{AB} = \left( {- 1;1;0} \right)$ ; $\overset{\rightarrow}{AC} = \left( {0; - 1;0} \right)$.
b) $AB = \sqrt{3};\, AC = 2$.
c) Góc $\widehat{BAC} = 45^{0}$.
d) Diện tích tam giác ABC bằng $\dfrac{1}{2}$.
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng.

Xét tính đúng, sai của các mệnh đề sau:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: $R = 90$ (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\dfrac{n}{4} = \dfrac{200}{4} = 50$.
c) $Q_{3} = \dfrac{17}{4}$.
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.
Sau khi tiêm một loại thuốc vào cơ thể bệnh nhân, nồng độ thuốc trong máu (tính theo $mg/cm^{3}$) thay đổi theo công thức $C(t) = \dfrac{0,15t}{t^{2} + 1}$, trong đó $t$ là thời gian (tính theo giờ) kể từ thời điểm tiêm thuốc, $t \geq 0$. Nồng độ thuốc trong máu đạt giá trị lớn nhất là bao nhiêu $mg/cm^{3}$ (kết quả làm tròn đến hàng phần trăm)?
Thầy An tham dự giải “Đi bộ trực tuyến Ngành Giáo dục và Đào tạo Edu Run – HCMC” năm 2024. Quãng đường thầy An đi được biểu diễn bằng hàm số \(s(t) = a{t^3} + b{t^2} + ct + d\) (với \(a \ne 0\)) có đồ thị như hình bên (trong đó t là thời gian tính bằng giờ, s là quãng đường tính bằng km). Khi đó, vận tốc tối đa của thầy An đạt được là bao nhiêu?

Trong không gian với hệ tọa độ Oxyz, cho $\Delta ABC$ biết A(2; 0; 0), B(0; 2; 0), C(1; 1; 3). $H(x_{0};y_{0};z_{0})$ là chân đường cao hạ từ đỉnh A xuống BC. Khi đó $x_{0} + y_{0} + z_{0}$ bằng (làm tròn đến hàng phần trăm)?
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(100; 50; 5) đến điểm B(200; 100; 10) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là C(x; y; z). Khi đó tính x + y + z.
Lời giải và đáp án
Cho hàm số y = f(x) có đồ thị như hình vẽ.

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
$(-\infty; 2)$.
-
B.
(1; 3).
-
C.
(0; 3).
-
D.
(0; 2).
Đáp án : D
Hàm số đồng biến trên khoảng đồ thị đi lên từ trái sang.
Hàm số đồng biến trên khoảng (0; 2).
Hàm số $y = x^3 - 3x - 2025$ nghịch biến trên khoảng nào dưới đây?
-
A.
$\left(-1; 1\right)$.
-
B.
$\left(0; 3\right)$.
-
C.
$\left(-\infty; -1\right)$.
-
D.
$\left(1; 3\right)$.
Đáp án : A
Xét dấu đạo hàm y’.
\(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\).
Hàm số là hàm đa thức bậc ba với a = 1 > 0 nên hàm số nghịch biến trên (-1;1).
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x^{4} - 2x^{2} - 1$ trên đoạn $\left\lbrack {- 1;2} \right\rbrack$. Giá trị của biểu thức M + 3m bằng
-
A.
1.
-
B.
5.
-
C.
6.
-
D.
4.
Đáp án : A
Cho hàm số y = f(x).
Bước 1: Tìm tập xác định.
Bước 2: Tính đạo f’(x). Tìm các giá trị \({x_1},{x_2},...,{x_n} \in [a;b]\) sao cho f’(x) = 0 hoặc f’(x) không tồn tại.
Bước 3: Tính \(f\left( a \right),f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( b \right)\). Giá trị lớn nhất trong các giá trị vừa tìm là \(\mathop {\max }\limits_{[a;b]} f(x)\), giá trị nhỏ nhất trong các giá trị vừa tìm là \(\mathop {\min }\limits_{[a;b]} f(x)\).
Ta có: \(f'\left( x \right) = 4{x^3} - 4x\).
Xét \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 1\end{array} \right.\)
Ta có f(-1) = -2; f(0) = -1; f(2) = 7.
Vậy M = 7, m = -2. Do đó M + 3m = 7 + 3(-2) = 1.
-
A.
$y = \dfrac{x^{2} - x - 1}{x - 2}$.
-
B.
$y = \dfrac{x^{2} - x + 1}{x + 2}$.
-
C.
$y = \dfrac{x^{2} - 2x - 1}{x - 2}$.
-
D.
$y = \dfrac{- x^{2} + x - 1}{x - 2}$.
Đáp án : A
Dựa vào tiệm cận đứng và giao điểm của đồ thị với trục hoành.
Tiệm cận đứng của đồ thị là x = 2 nên loại đáp án B.
Đồ thị cắt trục hoành tại hai điểm, giả sử hoành độ là \({x_1} < {x_2}\).
Quan sát đồ thị, ta thấy \( - 1 < {x_1} < 0\) và \(1 < {x_2} < 2\).
Do đó phương trình y = 0 có hai nghiệm \({x_1},{x_2}\) thỏa mãn điều kiện trên.
Thấy chỉ có phương trình \({x^2} - x - 1 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn.
Vậy đồ thị ở hình vẽ là của hàm số $y = \dfrac{x^{2} - x - 1}{x - 2}$.
Cho hình lập phương ABCD.A’B’C’D’. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
-
A.
\(\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
B.
\(\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
C.
\(\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
D.
\(\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
Đáp án : B
Áp dụng quy tắc hình hộp.
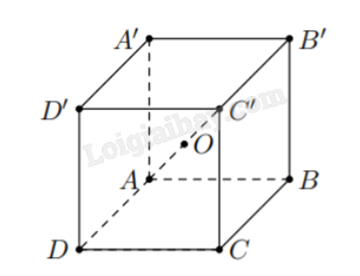
Áp dụng quy tắc hình hộp, ta có: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
Vì O là trung điểm của AC’ nên \(\overrightarrow {AO} = \frac{1}{2}\overrightarrow {AC'} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\).
Trong không gian Oxyz, O là gốc tọa độ, $\overrightarrow{OM} = - \overrightarrow{i} - 2\overrightarrow{k}$. Tọa độ của điểm M là
-
A.
(1; 0; -2).
-
B.
(1; 0; 2).
-
C.
(-1; -2; 0).
-
D.
(-1; 0; -2).
Đáp án : D
Tọa độ của điểm M là tọa độ $\overrightarrow{OM}$.
Tọa độ điểm M là (-1; 0; -2).
Trong không gian Oxyz, cho hai điểm A(3;-2;1) và B(4;2;3). Vecto $\overrightarrow{AB}$ có tọa độ là:
-
A.
(-1;0;2).
-
B.
(1;4;2).
-
C.
(1;0;2).
-
D.
(-1;-4;-2).
Đáp án : B
Với hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\), ta có \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
\(\overrightarrow {AB} = (4 - 3;2 + 2;3 - 1) = (1;4;2)\).
Cho \(\overrightarrow {AB} = \left( {1;3;2} \right)\). Tọa độ của \(\overrightarrow a = 2\overrightarrow {AB} \) là
-
A.
\(\left( {2;6;4} \right)\)
-
B.
\(\left( {2;3;4} \right)\)
-
C.
\(\left( {2;6;2} \right)\)
-
D.
\(\left( {1;6;4} \right)\)
Đáp án : A
Áp dụng biểu thức tọa độ nhân vecto với một số: \(\overrightarrow u = (a;b;c) \Rightarrow k\overrightarrow u = (ka;kb;kc)\).
\(\overrightarrow a = 2\overrightarrow {AB} = \left( {2.1;2.3;2.2} \right) = \left( {2;6;4} \right)\).
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (1; - 2;1)\) và \(\overrightarrow b = (2; - 4; - 2)\). Khi đó \(\overrightarrow a .\overrightarrow b \) bằng
-
A.
8
-
B.
-8
-
C.
12
-
D.
-12
Đáp án : A
\(\overrightarrow a .\overrightarrow b = {x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}\).
\(\overrightarrow a .\overrightarrow b = 1.2 - 2.( - 4) + 1.( - 2) = 8\).
Trong không gian Oxy, cho điểm A(-5;2;3) và B là điểm đối xứng với A qua trục Oy. Độ dài đoạn thẳng AB bằng
-
A.
\(\sqrt {34} \)
-
B.
\(\sqrt 8 \)
-
C.
\(2\sqrt {34} \)
-
D.
\(\sqrt {38} \)
Đáp án : C
Điểm A’ đối xứng với A(a;b;c) qua trục Oy có tọa độ (-a;b;-c).
Áp dụng công thức tính khoảng cách giữa hai điểm A, B: \(AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \).
B đối xứng với A qua Oy nên B(5;2;-3).
\(AB = \sqrt {{{(5 + 5)}^2} + {{(2 - 2)}^2} + {{( - 3 - 3)}^2}} = 2\sqrt {34} \).
Chiều cao của 40 học sinh lớp 12A được ghi lại như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng:
-
A.
30.
-
B.
5.
-
C.
25.
-
D.
20.
Đáp án : A
Lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên (chứa mẫu số liệu).
R = 177 - 147 = 30.
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 30 con hồ và thu được kết quả như sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là:
-
A.
1,38.
-
B.
1,27.
-
C.
2,3.
-
D.
1,71.
Đáp án : B
+) Phương sai mẫu, kí hiệu là ${{s}^{2}}$, được tính bởi công thức:
$S^2=\frac{1}{n}\left(n_1 x_1^2+n_2 x_2^2+\ldots+n_k x_k^2\right)-\bar{x}$.
trong đó $\mathrm{n}=\mathrm{n}_1+\mathrm{n}_2+\ldots+\mathrm{n}_{\mathrm{k}}$ và $\bar{x}$ là số trung bình mẫu.
+) Độ lệch chuẩn, kí hiệu $s$, là căn bậc hai của phương sai mẫu: $s=\sqrt{{{s}^{2}}}$.
\(\frac{{14.5 + 62 + 148.5 + 140 + 92.5 + 58.5}}{{30}} = \frac{{516}}{{30}} = 17,2\)
\(\bar z = \frac{{516}}{{30}} = 17.2\)
\({s^2} = \frac{1}{{30}}\left[ {1.14,{5^2} + 4.15,{5^2} + 9.16,{5^2} + 8.17,{5^2} + 5.18,{5^2} + 3.19,{5^2}} \right] - 17,{2^2} = \frac{{161}}{{100}}\).
\(s = \frac{{\sqrt {161} }}{{100}} \approx 1,27\).
Trong không gian $Oxyz$ cho các điểm $A\left( {5;1;3} \right);\, B\left( {4;2;3} \right);\, C\left( {5;0;3} \right)$.
a) $\overset{\rightarrow}{AB} = \left( {- 1;1;0} \right)$ ; $\overset{\rightarrow}{AC} = \left( {0; - 1;0} \right)$.
b) $AB = \sqrt{3};\, AC = 2$.
c) Góc $\widehat{BAC} = 45^{0}$.
d) Diện tích tam giác ABC bằng $\dfrac{1}{2}$.
a) $\overset{\rightarrow}{AB} = \left( {- 1;1;0} \right)$ ; $\overset{\rightarrow}{AC} = \left( {0; - 1;0} \right)$.
b) $AB = \sqrt{3};\, AC = 2$.
c) Góc $\widehat{BAC} = 45^{0}$.
d) Diện tích tam giác ABC bằng $\dfrac{1}{2}$.
a) Với hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\), ta có \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
b) Cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\), \(B\left( {{x_B};{y_B};{z_B}} \right)\). Độ dài vecto \(\overrightarrow {AB} \) hay khoảng cách từ A đến B là: \(\left| {\overrightarrow {AB} } \right| = AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
c) Để tính góc \(\alpha \) giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), ta sử dụng công thức:
\(\cos \alpha = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}}}{{\sqrt {{x_a}^2 + {y_a}^2 + {z_a}^2} .\sqrt {{x_b}^2 + {y_b}^2 + {z_b}^2} }}\).
d) Áp dụng công thức \({S_{ABC}} = \frac{1}{2}bc\sin A\).
a) Đúng. \(\overrightarrow {AB} = (4 - 5;2 - 1;3 - 3) = ( - 1;1;0)\), \(\overrightarrow {AC} = (5 - 5;0 - 1;3 - 3) = (0; - 1;0)\).
b) Sai. \(AB = \sqrt {{{( - 1)}^2} + {1^2} + {0^2}} = \sqrt 2 \), \(AC = \sqrt {{0^2} + {{( - 1)}^2} + {0^2}} = 1\).
c) Sai. \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{ - 1.0 + 1.( - 1) + 0.0}}{{\sqrt 2 .1}} = - \frac{{\sqrt 2 }}{2} \Rightarrow \widehat {BAC} = {135^o}\).
d) Đúng. \({S_{ABC}} = \frac{1}{2}AB.AC\sin \widehat {BAC} = \frac{1}{2}.\sqrt 2 .1.\sin {135^o} = \frac{1}{2}\).
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng.

Xét tính đúng, sai của các mệnh đề sau:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: $R = 90$ (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\dfrac{n}{4} = \dfrac{200}{4} = 50$.
c) $Q_{3} = \dfrac{17}{4}$.
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: $R = 90$ (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\dfrac{n}{4} = \dfrac{200}{4} = 50$.
c) $Q_{3} = \dfrac{17}{4}$.
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.
Khoảng biến thiên, kí hiệu R, của mẫu số liệu ghép nhóm là hiếu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu của mẫu số liệu.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó.
a) Sai. Khoảng biến thiên: R = 90 – 10 = 80.
b) Đúng. Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = 150\).
c) Sai. \({Q_3} = 50 + \frac{{\frac{{3.200}}{4} - (18 + 31 + 40 + 48)}}{{50}}.(60 - 50) = 52,6\).
d) Đúng. \({Q_1} = 30 + \frac{{\frac{{200}}{4} - (18 + 31)}}{{40}}.(40 - 30) = 30,25\).
\({\Delta _Q} = {Q_3} - {Q_1} = 52,6 - 30,25 = 22,35 > 20\).
Sau khi tiêm một loại thuốc vào cơ thể bệnh nhân, nồng độ thuốc trong máu (tính theo $mg/cm^{3}$) thay đổi theo công thức $C(t) = \dfrac{0,15t}{t^{2} + 1}$, trong đó $t$ là thời gian (tính theo giờ) kể từ thời điểm tiêm thuốc, $t \geq 0$. Nồng độ thuốc trong máu đạt giá trị lớn nhất là bao nhiêu $mg/cm^{3}$ (kết quả làm tròn đến hàng phần trăm)?
Tính đạo hàm, lập bảng biến thiên.
Ta có \({C^\prime }(t) = \frac{{0,15\left( {1 - {t^2}} \right)}}{{{{\left( {{t^2} + 1} \right)}^2}}},t \ge 0\).
Bảng biến thiên của hàm số \(C(t)\) trên \((0; + \infty )\):

Dựa vào bảng biến thiên, ta thấy nồng độ thuốc trong máu đạt giá trị lớn nhất bằng 0,08 mg/\(c{m^3}\).
Thầy An tham dự giải “Đi bộ trực tuyến Ngành Giáo dục và Đào tạo Edu Run – HCMC” năm 2024. Quãng đường thầy An đi được biểu diễn bằng hàm số \(s(t) = a{t^3} + b{t^2} + ct + d\) (với \(a \ne 0\)) có đồ thị như hình bên (trong đó t là thời gian tính bằng giờ, s là quãng đường tính bằng km). Khi đó, vận tốc tối đa của thầy An đạt được là bao nhiêu?

Dựa vào các điểm đồ thị đi qua, lập hệ phương trình, giải để tìm hệ số a, b, c, d của hàm số s(t). Từ đó suy ra hàm số v(t).
Ứng dụng đạo hàm, tìm GTLN của hàm số v(t).
\(v(t) = s'(t) = 3a{t^2} + 2bt + c\).
Quan sát hình vẽ, thấy đồ thị hàm số s(t) đi qua các điểm có tọa độ (0;0), (2;12), (4;24) nên ta có s(0) = 0, s(2) = 12, s(4) = 24.
Mặt khác, hàm số đạt cực trị tại x = 4 nên s’(4) = 0.
Ta có hệ: \(\left\{ \begin{array}{l}s(0) = 0\\s(2) = 12\\s(4) = 24\\s'(4) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a{.0^3} + b{.0^2} + c.0 + d = 0\\a{.2^3} + b{.2^2} + c.2 + d = 12\\a{.4^3} + b{.4^2} + c.4 + d = 24\\3a{.4^2} + 2b.4 + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{3}{4}\\b = \frac{9}{2}\\c = 0\\d = 0\end{array} \right.\)
Suy ra \(s(t) = - \frac{3}{4}{t^3} + \frac{9}{2}{t^2}\); \(v(t) = - \frac{9}{4}{t^2} + 9t\).
Để tìm vận tốc tối đa thầy An đạt được, ta cần tìm GTLN của hàm số \(v(t) = - \frac{9}{4}{t^2} + 9t\).
Ta có \(v'(t) = 0 \Leftrightarrow - \frac{9}{2}t + 9 = 0 \Leftrightarrow t = 2\).
Bảng biến thiên:

Vậy tốc độ tối đa thầy An đạt được là 9 km/h.
Trong không gian với hệ tọa độ Oxyz, cho $\Delta ABC$ biết A(2; 0; 0), B(0; 2; 0), C(1; 1; 3). $H(x_{0};y_{0};z_{0})$ là chân đường cao hạ từ đỉnh A xuống BC. Khi đó $x_{0} + y_{0} + z_{0}$ bằng (làm tròn đến hàng phần trăm)?
Vì B, C, H thẳng hàng nên $\overset{\rightarrow}{BH} = t\overset{\rightarrow}{BC}$, từ đó biểu diễn tọa độ điểm H theo t.
Giải $\left. \overset{\rightarrow}{AH}\bot\overset{\rightarrow}{BC}\Leftrightarrow\overset{\rightarrow}{AH} \cdot \overset{\rightarrow}{BC} = 0 \right.$ tìm t, từ đó suy ra tọa độ điểm H.
$\overset{\rightarrow}{BC} = (1; - 1;3)$, $\overset{\rightarrow}{BH}(x_{0};y_{0} - 2;z_{0})$.
Vì B, C, H thẳng hàng nên $\overset{\rightarrow}{BH} = t\overset{\rightarrow}{BC}$, $t \in R$. Ta có $\left\{ \begin{array}{l} {x_{0} = t} \\ {y_{0} - 2 = - t} \\ {z_{0} = 3t} \end{array} \right.$ $\left( {t \in {\mathbb{R}}} \right)$.
$H(t;2 - t;3t) \in BC$. Khi đó: $\overset{\rightarrow}{AH} = (t - 2;2 - t;3t)$.
Mà H là chân đường cao hạ từ đỉnh A xuống BC nên:
$\left. \overset{\rightarrow}{AH}\bot\overset{\rightarrow}{BC}\Leftrightarrow\overset{\rightarrow}{AH} \cdot \overset{\rightarrow}{BC} = 0\Leftrightarrow t - 2 - 2 + t + 9t = 0\Leftrightarrow t = \dfrac{4}{11} \right.$.
$\left. \Rightarrow H\left( {\dfrac{4}{11};\dfrac{18}{11};\dfrac{12}{11}} \right)\Rightarrow x_{0} + y_{0} + z_{0} = \dfrac{34}{11} \approx 3,09 \right.$.
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(100; 50; 5) đến điểm B(200; 100; 10) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là C(x; y; z). Khi đó tính x + y + z.
Gọi C(x; y; z) là tọa độ của máy bay sau 10 phút tiếp theo.
Giải phương trình $\overset{\rightarrow}{AB} = \overset{\rightarrow}{BC}$ tìm tọa độ C.

Gọi C(x; y; z) là tọa độ của máy bay sau 10 phút tiếp theo.
$\overset{\rightarrow}{AB} = (100;50;5)$, $\overset{\rightarrow}{BC} = (x - 200;y - 100;z - 10)$.
Vì máy bay giữ nguyên hướng bay nên $\overset{\rightarrow}{AB}$ và $\overset{\rightarrow}{BC}$ cùng hướng.
Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ A đến B bằng thời gian bay từ B đến C nên $\overset{\rightarrow}{AB} = \overset{\rightarrow}{BC}$.
Suy ra $\left. \overset{\rightarrow}{AB} = \overset{\rightarrow}{BC}\Leftrightarrow\left\{ \begin{array}{l} {100 = x - 200} \\ {50 = y - 100} \\ {5 = z - 10} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {x = 300} \\ {y = 150} \\ {z = 15} \end{array} \right.\Rightarrow C(300;150;15) \right.$.
Tọa độ của máy bay sau 10 phút tiếp theo là C(300; 150; 15).
Vậy x + y + z = 300 + 150 + 15 = 465.
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
1) TXĐ: \(D = \mathbb{R}\backslash \{ 2\} \).
2) Sự biến thiên:
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to {2^ - }} y = + \infty \); \(\mathop {\lim }\limits_{x \to {2^ + }} y = - \infty \). Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = - 2\); \(\mathop {\lim }\limits_{x \to - \infty } y = - 2\). Do đó, đường thẳng y = -2 là tiệm cận ngang của đồ thị hàm số.
Đạo hàm: \(y' = \frac{{10}}{{{{( - x + 2)}^2}}} > 0\), với mọi \(x \ne 2\).
Bảng biến thiên:
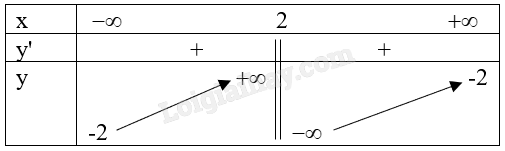
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\), \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
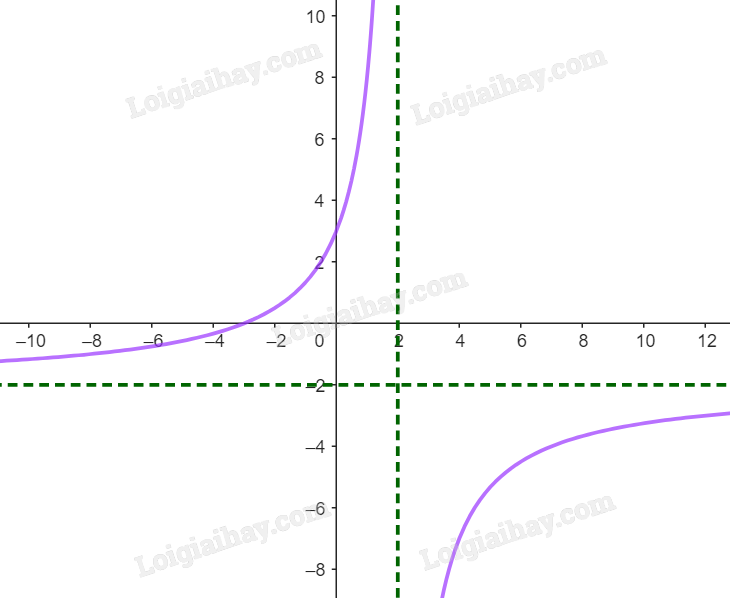
3) Đồ thị:
- Giao điểm của đồ thị với trục tung: (0;3).
- Giao điểm của đồ thị với trục hoành: (-3;0).
- Đồ thị hàm số đi qua các điểm (0;3), (-3;0), (4;-7) và (7;-4).
- Đồ thị hàm số nhận giao điểm (2;-2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Ta vẽ được đồ thị \(y = \frac{{2x + 6}}{{ - x + 2}}\) như hình:
Áp dụng tính chất phân phối của vecto.
Để tính tích vô hướng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) trong không gian, ta áp dụng công thức:
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Ta có \(\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) . \overrightarrow {BC} \)
\(= \overrightarrow {AB} . \overrightarrow {BC} + \overrightarrow {AD} . \left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \)
\(= \overrightarrow {AB} . \overrightarrow {BC} + \overrightarrow {AD} . \overrightarrow {AC} - \overrightarrow {AD} . \overrightarrow {AB} \)
\(= a . a . \cos {120^ \circ } + a . a . \cos {60^ \circ } - a . a . \cos {60^ \circ } \)
\(= - \frac{{{a^2}}}{2}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\({S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\)
\(= \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\).
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).
Ta có bảng sau:

Cỡ mẫu \(n = 9 + 15 + 12 + 4 = 40\).
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{9.4,95 + 15.5,05 + 12.5,15 + 4.5,25}}{{40}} = \frac{{2031}}{{400}} = 5,0775\).
Phương sai của mẫu số liệu ghép nhóm đó là:
\({S^2} = \frac{1}{{40}}\left( {{{9.4,95}^2} + {{15.5,05}^2} + {{12.5,15}^2} + {{4.5,25}^2}} \right) - {5,0775^2} \approx 0,0085\).
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S = \sqrt {0,0085} \approx 0,09\).
Đề thi học kì 1 Toán 12 - Đề số 9
Đề thi học kì 1 Toán 12 - Đề số 10
Đề thi học kì 1 Toán 12 - Đề số 7
Đề thi học kì 1 Toán 12 - Đề số 6
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số 1. Tính đơn điệu và cực trị của hàm số 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3. Đường tiệm cận của đồ thị hàm số 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn












Danh sách bình luận