-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Ôn tập chương I
Câu 9 trang 35 SGK Hình học 11 Nâng cao
Cho đường tròn (O ; R)
Đề bài
Cho đường tròn (O ; R) và điểm A cố định. Một dây cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Lời giải chi tiết
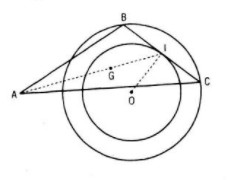
Gọi I là trung điểm của BC thì \(OI\bot BC\)
Ta có
\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \cr
& \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {GI} = \overrightarrow 0 \cr
& \Leftrightarrow \overrightarrow {AG} = {2 \over 3}\overrightarrow {AI} \cr} \)
Tức là phép vị tự V tâm A tỉ số \({2 \over 3}\) biến điểm I thành điểm G
Trong tam giác vuông OIB ta có:
\(OI = \sqrt {O{B^2} - I{B^2}} \)\(= \sqrt {{R^2} - {{\left( {{m \over 2}} \right)}^2}} = R'\) (không đổi)
Nên quỹ tích I là đường tròn (O ; R’) hoặc là điểm O (nếu m = 2R)
Do đó quỹ tích G là ảnh của quỹ tích I qua phép vị tự V
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 8 trang 35 SGK Hình học 11 Nâng cao
- Câu 7 trang 34 SGK Hình học 11 Nâng cao
- Câu 6 trang 34 SGK Hình học 11 Nâng cao
- Câu 5 trang 34 SGK Hình học 11 Nâng cao
- Câu 4 trang 34 SGK Hình học 11 Nâng cao .
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
