-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Câu hỏi và bài tập ôn tập chương V
Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao
Cho parabol (P) :
Đề bài
Cho parabol (P) : \(y = {x^2}.\) Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = -2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.
Lời giải chi tiết
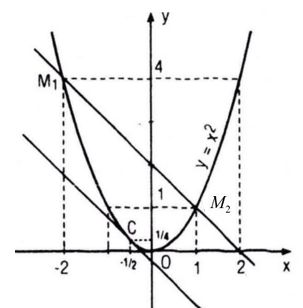
Các điểm M1 và M2 có tọa độ là M1(-2 ; 4); M2(1 ; 1)
Hệ số góc của cát tuyến M1M2 là \(\tan \varphi = {{\Delta y} \over {\Delta x}} = {{4 - 1} \over { - 2 - 1}} = - 1\)
Vì tiếp tuyến tại điểm \(C\left( {{x_0};x_0^2} \right)\) song song với cát tuyến M1M2 nên ta có :
\(y'\left( {{x_0}} \right) = - 1 \Leftrightarrow 2{x_0} = - 1 \Leftrightarrow {x_0} = {{ - 1} \over 2},\)
Suy ra tọa độ của điểm C là \(\left( { - {1 \over 2};{1 \over 4}} \right)\)
Vậy phương trình tiếp tuyến phải tìm là :
\(y = \left( { - 1} \right)\left( {x + {1 \over 2}} \right) + {1 \over 4} \Leftrightarrow y = - x - {1 \over 4}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 57 trang 222 SGK Đại số và Giải tích 11 Nâng cao
- Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao
- Câu 54 trang 221 SGK Đại số và Giải tích 11 Nâng cao
- Câu 53 trang 221 SGK Đại số và Giải tích 11 Nâng cao
- Câu 52 trang 221 SGK Đại số và Giải tích 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
