Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo biết rằng:
-
A.
-
B.
-
C.
-
D.
- Áp dụng định lí: Góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
- Tính chất: Hai góc kề bù có tống số đo bằng
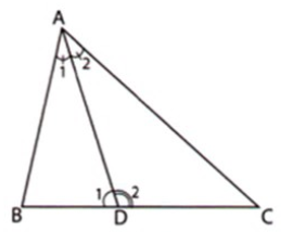
Ta có: là góc ngoài tại đỉnh của tam giác nên
Ta có: là góc ngoài tại đỉnh của tam giác nên
Từ (1) và (2) ta có:
Vì là tia phân giác nên và suy ra
Mặt khác và là hai góc kề bù nên
Từ (3) và (4) suy ra
Vậy
Đáp án : C

Các bài tập cùng chuyên đề
Tổng ba góc của một tam giác bằng
Cho tam giác vuông tại . Khi đó
Cho tam giác có . Số đo góc là:
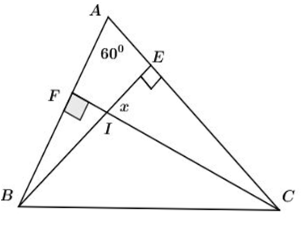
Cho hình vẽ sau. Tính số đo
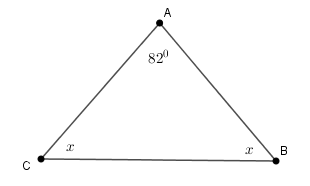
Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc .
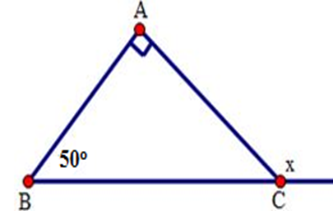
Cho hình sau. Tính số đo
Cho tam giác biết rằng số đo các góc tỉ lệ với . Tính
Tam giác có . Số đo góc và góc lần lượt là:
Cho tam giác có Tia phân giác của góc C cắt cạnh AB tại M. Tính và
Cho tam giác ABC có Tính và
Cho hình vẽ sau. Tính số đo góc