-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Bài 5.17 trang 148 SGK Toán 11 tập 1 - Cùng khám phá
Để chuẩn bị cho đồ án tốt nghiệp, một sinh viên y khoa đã khảo sát huyết áp tối đa của một số bệnh nhân và lập được bảng tần số ghép nhóm sau:
Đề bài
Để chuẩn bị cho đồ án tốt nghiệp, một sinh viên y khoa đã khảo sát huyết áp tối đa của một số bệnh nhân và lập được bảng tần số ghép nhóm sau:
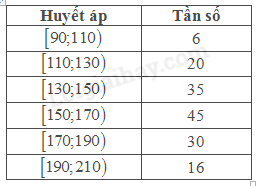
a) Xác định trung bình, trung vị và mốt của mẫu số liệu.
b) Hãy giải thích vì sao trong trường hợp này, cả ba giá trị tìm được đều đại diện tốt cho huyết áp của những bệnh nhân được khảo sát.
Phương pháp giải - Xem chi tiết
+) \(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
+) Trung vị \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\) trong đó \({L_m},{n_m},h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị. \(T\) là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.
+) Công thức tìm mốt của mẫu số liệu ghép nhóm là \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Lời giải chi tiết
a)
+) Xác định trung bình
Để ngắn gọn, ta lập bảng sau
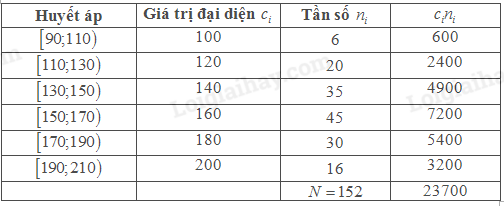
Áp dụng công thức tính trung bình ta có \(\overline x = \frac{{23700}}{{152}} \approx 156\)
+) Xác định trung vị
Ta có bảng tần số tích lũy sau
Ta có \(\frac{N}{2} = \frac{{152}}{2} = 76\). Nhóm đầu tiên có tần số tích lũy lớn hơn bằng 76 là \(\left[ {150;170} \right)\)
Ta có \({L_m} = 150\), \(h = 170 - 150 = 20\), \({n_m} = 45\) và \(T = 61\).
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 150 + \frac{{76 - 61}}{{45}}.20 \approx 157\)
+) Xác định mốt
Dựa vào bảng dữ liệu ta có nhóm chứa mốt là \(\left[ {150;170} \right)\) với tần số là 45.
Do đó \({L_m} = 150;h = 170 - 150 = 20;a = 45 - 35 = 10;b = 45 - 30 = 15\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 150 + \frac{{10}}{{10 + 15}}.20 = 158\)
b) Dựa vào ba giá trị tìm được \(\overline x = 156,{M_e} = 157,{M_0} = 158\) ta nhận thấy cả ba giá trị tìm được đều đại diện tốt cho huyết áp của những bệnh nhân được khảo sát là vì ba giá trị này xấp xỉ bằng nhau và huyết áp của người bình thường cũng trong khoảng 150 đến 170
Bình luận
Chia sẻ
- Bài 5.18 trang 148 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 5.19 trang 148 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 5.20 trang 149 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 5.21 trang 149 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 5.22 trang 149 SGK Toán 11 tập 1 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
