-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Bài 4.30 trang 124 SGK Toán 11 tập 1 - Cùng khám phá
Cho hình chóp S.ABC. Gọi G, K, H lần lượt là trọng tâm của các tam giác SAB, SBC, ABC.
Đề bài
Cho hình chóp S.ABC. Gọi G, K, H lần lượt là trọng tâm của các tam giác SAB, SBC, ABC.
a) Chứng minh GK // (ABC).
b) Tìm giao tuyến của (BGK) và (ABC).
Phương pháp giải - Xem chi tiết
a) Nếu đường thẳng d không nằm trong (P) song song với đường thẳng a nằm trong (P) thì d song song với (P).
b) (P) và (Q) có điểm chung A và chứa lần lượt 2 đường thẳng a, b song song với nhau thì có giao tuyến d là đường thẳng đi qua A và song song với a, b.
Lời giải chi tiết
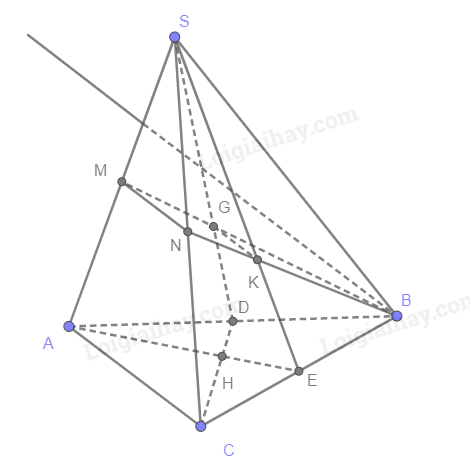
a) Gọi M, N lần lượt là trung điểm của SA, SC
Xét tam giác SAC có M, N lần lượt là trung điểm của SA, SC nên MN // AC (1)
G, K lần lượt là trọng tâm của tam giác SAB, SBC nên \(\frac{{BG}}{{BM}} = \frac{{BK}}{{BN}} = \frac{2}{3}\). Suy ra GK // MN (2)
Từ (1), (2) suy ra GK // AC. Mà AC nằm trong (ABC)
Vậy GK // (ABC)
b) (ABC) và (BGK) có chung điểm B, GK // AC nên giao tuyến của (ABC) và (BGK) là đường thẳng đi qua B, song song với GK, AC.
Bình luận
Chia sẻ
- Bài 4.31 trang 124 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 4.32 trang 124 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 4.33 trang 124 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 4.34 trang 124 SGK Toán 11 tập 1 - Cùng khám phá
- Bài 4.35 trang 125 SGK Toán 11 tập 1 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
