Bài 3.4: Độ tập trung và phân tán của dữ liệu - Chuyên đề Tin học 12 Chân trời sáng tạo

Câu 1

Trả lời câu hỏi khởi động trang 80 Chuyên đề Tin học 12 Chân trời sáng tạo

Quan sát Bảng 1, em có nhận xét gì về điểm của ba môn Toán, Ngữ văn, Ngoại ngữ?

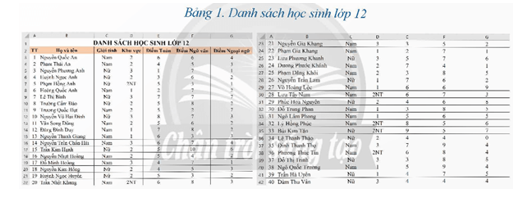
Lời giải chi tiết:

Quan sát Bảng 1, em có nhận xét về điểm của ba môn Toán, Ngữ văn, Ngoại ngữnhư sau:

- Ngoại ngữ: đa dạng về điểm số, khả năng ngoại ngữ giữa học sinh rất khác nhau.

- Ngữ văn: có sự chênh lệch về điểm số giữa các học sinh.

- Toán: Điểm số có sự biến đổi, với một số học sinh đạt điểm cao trong khi một số khác thấp hơn.

1 Câu 1

Trả lời câu hỏi 1 trang 82 Chuyên đề Tin học 12 Chân trời sáng tạo

Hàm nào dùng để tính giá trị trung bình cộng của các số trong mẫu số liệu

Lời giải chi tiết:

Hàm dùng để tính giá trị trung bình cộng của các số trong mẫu số liệu là hàm AVERAGE:

Cú pháp: AVERAGE(number1, [number2], ...)

 Trong đó: number1, number2, ...: Các số hoặc phạm vi chứa các số mà bạn muốn tính trung bình cộng.

1 Câu 2

Trả lời câu hỏi 2 trang 82 Chuyên đề Tin học 12 Chân trời sáng tạo

Hàm nào dùng để trả về giá trị có tần số lớn nhất trong một bảng tần số

Lời giải chi tiết:

Hàm dùng để trả về giá trị có tần số lớn nhất trong một bảng tần số là: MODE.SNGL hoặc MODE.MULT.

Cú pháp: MODE.SNGL(number1, [number2], ...)

Trong đó:number1, number2, ...: Các số hoặc phạm vi chứa các số mà bạn muốn tìm giá trị xuất hiện nhiều nhất.

2 Câu 1

Trả lời câu hỏi 1 trang 83 Chuyên đề Tin học 12 Chân trời sáng tạo

Các hàm nào dùng để tính phương sai và độ lệch chuẩn?

Lời giải chi tiết:

1. Các hàm sau dùng để tính phương sai và độ lệch chuẩn:

- Chức năng: Hàm tính phương sai dựa trên toàn bộ tập hợp (bỏ qua các giá trị logic và văn bản).

- Cú pháp: =VAR.P(number1, [number2],...).

Trong đó:

number1: Tham chiếu ô tính, tên vùng hoặc phạm vi thứ nhất chứa số (Đối số bắt buộc). 

[number2]: Tham chiếu ô tính, tên vùng hoặc phạm vi thứ hai chứa số (Đối số tuỳ chọn).

2. Các hàm sau dùng để tính độ lệch chuẩn:

- Chức năng: Hàm tính độ lệch chuẩn dựa trên toàn bộ tập hợp (bỏ qua các giá trị logic và văn bản).

- Cú pháp: =STDEV.P(number1, [number2],...).

Trong đó:

number1: Tham chiếu ô tính, tên vùng hoặc phạm vi thứ nhất chứa sổ (Đối số bắt buộc).

[number2]: Tham chiếu ô tính, tên vùng hoặc phạm vi thứ hai chứa số (Đối số tuỳ chọn).

1 Câu 2

Trả lời câu hỏi 2 trang 83 Chuyên đề Tin học 12 Chân trời sáng tạo

Để tính hệ số biến thiên em sử dụng kết hợp các hàm nào?

Lời giải chi tiết:

Để tính hệ số biến thiên em sử dụng kết hợp các hàm:

- Hệ số biến thiên là một thước đo thống kê độ phân tán của các dữ liệu trong một chuỗi dữ liệu so với giá trị trung bình.

- Hệ số biến thiên (Co-efficient of Variation (CV), được tính bằng công thức: CV = ‡ × 100

với S là độ lệch chuẩn, x là giá trị trung bình.

- Để tính hệ số biến thiên trong bảng tính, em sử dụng các hàm STDEV.P và AVERAGE.

Luyện tập Câu 1

Trả lời câu hỏi Luyện tập 1 trang 83 Chuyên đề Tin học 12 Chân trời sáng tạo

Hàm nào là hàm trả về số đứng giữa một bộ dữ liệu số?

A. AVERAGE.

B. MEDIAN.

C. QUARTILE.

D. MODE.

Lời giải chi tiết:

Hàm nào là hàm trả về số đứng giữa một bộ dữ liệu số:

Hàm MEDIAN là hàm trong Excel dùng để trả về giá trị ở vị trí giữa của một tập dữ liệu số đã được sắp xếp theo thứ tự tăng dần.

Cú pháp: =MEDIAN(number1, [number2], ...)

Trong đó: number1, number2, ... là các số hoặc phạm vi chứa các số mà bạn muốn tính giá trị trung vị (median).

Vậy đáp án đúng là:  B. MEDIAN.

Luyện tập Câu 2

Trả lời câu hỏi Luyện tập 2 trang 83 Chuyên đề Tin học 12 Chân trời sáng tạo

Hàm nào là hàm trả về tứ phân vị của tập dữ liệu?

A. AVERAGE.

B. MEDIAN.

C. QUARTILE.

D. MODE.

Lời giải chi tiết:

- QUARTILE là hàm trong Excel dùng để tính các giá trị tứ phân vị của một tập dữ liệu số.

Cú pháp =QUARTILE(array, quart)

Trong đó:

- array: Là mảng hoặc phạm vi chứa các số mà bạn muốn tính tứ phân vị.

- quart: Là số từ 0 đến 4, chỉ ra tứ phân vị cần tính (0 = Tứ phân vị thứ nhất, 1 = Tứ phân vị thứ hai, 2 = Median, 3 = Tứ phân vị thứ ba, 4 = Tứ phân vị thứ tư).

 Vậy đáp án đúng là:  C. QUARTILE.

Luyện tập Câu 3

Trả lời câu hỏi Luyện tập 3 trang 83 Chuyên đề Tin học 12 Chân trời sáng tạo

Hàm nào là hàm trả về giá trị có tần số lớn nhất của một bảng tần số?

A. AVERAGE.

B. MEDIAN.

C. QUARTILE.

D. MODE.

Lời giải chi tiết:

Hàm nào là hàm trả về giá trị có tần số lớn nhất của một bảng tần số?

A. AVERAGE.

B. MEDIAN.

C. QUARTILE.

D. MODE.

Nhiệm vụ Câu 1

Trả lời câu hỏi Nhiệm vụ 1 trang 84 Chuyên đề Tin học 12 Chân trời sáng tạo

Tính các đặc trưng về độ tập trung của dữ liệu

Yêu cầu: Sử dụng dữ liệu Bảng 1, tính các đặc trưng về độ tập trung của dữ liệu điểm môn Toán, môn Ngữ văn và môn Ngoại ngữ. Từ kết quả thu được, em có nhận xét gì về phân bố điểm của ba môn học này? tính các đặc trưng về độ tập trung của dữ liệu điểm môn Toán, môn Ngữ văn và môn Ngoại ngữ

Lời giải chi tiết:

Em sử dụng hàm AVERAGE để tính trung bình cộng, sử dụng hàm MODE.MUTL để tìm mốt, sử dụng hàm MEDIAN để tính trung vị và sử dụng hàm QUARTILE.EXC để tính tứ phân vị. Các bước thực hiện như sau:

- Tại ô tính chứa kết quả trung bình cộng điểm Toán (V4), nhập công thức=AVERAGE(E2:E42) (với E2:E42 là vùng dữ liệu của cột Điểm Toán).

- Tại ô tính chứa kết quả trung vị điểm Toán (V5), nhập công thức =MEDIAN(E2:E42).

- Tại ô tính chứa kết quả mốt điểm Toán (V6), nhập công thức =MODEMULT(E2:E42).

- Tại ô tính chứa kết quả tứ phân vị thứ nhất (W9), nhập công thức =QUARTILE.EXC($E$2:$E$42,V9) (với $E$2:$E$42 là vùng dữ liệu của cột Điểm Toán được chuyển sang dạng địa chỉ tuyệt đối) và thực hiện sao chép công thức cho các ô tính W10, W11 để tính tứ phân vị thứ hai và tứ phân vị thứ ba (Hình 1).

Kết quả trung bình cộng, trung vị, mốt và tứ phân vị của môn Toán như Hình 2.

2. Thực hiệnt tương tự cách tính trung bình cộng, trung vị, mốt, tứ phân vị như ở (1) để tính các đặc trưng cho vùng dữ liệu của cột Điểm Ngữ văn và điểm Ngoại ngữ. Kết quả như sau:

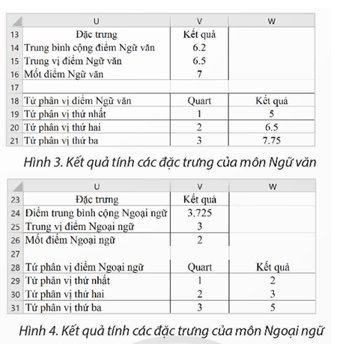
* Nhận xết về sự phân bố của ba môn học này: Căn cứ vào kết quả tính điểm trung bình cộng, trung vị, mốt, tứ phân vị và quan sát các biểu đồ cho thấy rằng phổ điểm môn Toán đối xứng phân bố đều, phổ điểm 2 môn Ngữ văn và môn Ngoại ngữ phân bố không đều.

Nhiệm vụ Câu 2

Trả lời câu hỏi Nhiệm vụ 2 trang 86 Chuyên đề Tin học 12 Chân trời sáng tạo

Tính các đặc trưng về độ phần tán của dữ liệu bởi khoảng biến thiên và phương sai

Yêu cầu: Sử dụng dữ liệu ở Bảng 1, học sinh học môn nào đồng đều hơn giữa môn Ngũ văn và môn Ngoại ngữ?

Lời giải chi tiết:

Để xác định học sinh học môn nào đồng đều hơn giữa môn Ngữ văn và môn Ngoại ngữ, em cần tính khoảng biển thiên và phương sai của điểm môn Ngữ văn và môn Ngoại ngữ. Nếu khoảng biến thiên và phương sai của môn nào nhỏ hơn thì môn đỏ được kết luận đồng đều hơn. Để thực hiện, em sử dụng hàm MAX, MIN để tìm khoảng biến thiên và VAR.P để tìm phương sai. Các bước thực hiện như sau;

1. Tính khoảng biến thiên của môn Ngữ văn, Ngoại ngữ.

Tại ô tính chứa kết quả (J3), nhập công thức =MAX(T2:F12)-MIN(F2:F12) dễ tính khoảng biến thiên của môn Ngữ văn. Thực hiện tương tự để tính khoảng biến thiên của môn Ngoại ngữ. Kết quả như Hình 7

2. Tính phương sai của môn Ngữ văn, Ngoại ngữ.

Tại ô tính chứa kết quả (J6), nhập công thức =VAR.P(F2:F42) để tính phương sai của môn Ngữ văn. Thực hiện tương tự để tính phương sai của môn Ngoại ngữ. Kết quả như Hình 8.

Căn cứ vào kết quả, khoảng biến thiên và phương sai của môn Ngữ văn nhỏ hơn của môn Ngoại ngữ nên học sinh học môn Ngữ văn đồng đều hơn.

Nhiệm vụ Câu 3

Trả lời câu hỏi Nhiệm vụ 3 trang 87 Chuyên đề Tin học 12 Chân trời sáng tạo

Tính các đặc trưng về độ phân tán của dữ liệu bởi độ lệch chuẩn và hệ số biến thiên.

Lời giải chi tiết:

Để biết mức độ đồng đều của điểm Ngữ văn và điểm Ngoại ngữ, em tìm hệ số biến thiên cho từng môn. Để xác định hệ số biến thiên, em tính độ lệch chuẩn và trung bình cộng của từng môn. Khi đó, nếu hệ số biến thiên của môn nào cao hơn thì điểm số có sự biến động. Em sử dụng hàm STDEV.P để tìm độ lệch chuẩn và hàm AVERAGE để tính trung bình cộng. Các bước thực hiện như sau:

1. Điểm Ngữ văn: Tại ô tính J4, nhập công thức =STDEV.P(F2:F42) để tính độ lệch chuẩn; tại ô tính K4, nhập công thức =AVERAGE(F2:F42) để tính trung bình cộng; tại ô tính L4, nhập công thức =J4/K4*100 để tính hệ số biến thiên (Hình 9).

2. Thực hiện tương tự để tính độ lệch chuẩn, trung bình cộng, hệ số biến thiên của điểm Ngoại ngữ.

3. Hiệu chỉnh và định dạng được kết quả như Hình 10.

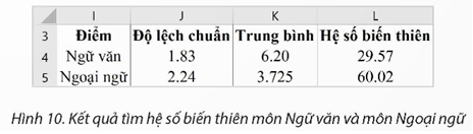
Như vậy, điểm Ngữ văn và điểm Ngoại ngữ có chênh lệch đáng kể trong phân bố điểm số và có độ biến động cao. Mức độ đồng đều của điểm số trong hai môn học này không cao và có sự biến thiên đáng kể. Đặc biệt, môn Ngoại ngữ có hệ số biến thiên cao hơn rất nhiều so với môn Ngữ văn, cho thấy điểm Ngoại ngữ có sự biến động lớn hơn và không đồng đều so với điểm Ngữ văn.

Vận dụng Câu 1

Trả lời câu hỏi Vận dụng 1 trang 88 Chuyên đề Tin học 12 Chân trời sáng tạo

Tiền lương hàng tháng (đơn vị: USD) của 15 nhân viên trong một công ty công nghệ được cho trong bảng sau:

Em hãy tính hai đặc trưng về độ tập trung của dữ liệu: Số trung bình và Trung vị. Dựa vào kết quả vừa tìm được, kết quả nào phù hợp để đại diện cho mức lương? Giải thích?

Lời giải chi tiết:

Tiền lương hàng tháng (đơn vị: USD) của 15 nhân viên trong một công ty công nghệ được cho trong bảng sau:

* Muốn tính số trung bình và trung vị của tiền lương hàng tháng, bạn có thể làm theo các bước sau trong Excel:

- Nhập dữ liệu lương vào một cột trong Excel.

- Sử dụng công thức =AVERAGE(range) để tính số trung bình, trong đó range là phạm vi chứa dữ liệu lương.

- Sử dụng công thức =MEDIAN(range) để tính trung vị.

Số trung bình là tổng của tất cả các giá trị chia cho số lượng giá trị. Trung vị là giá trị ở giữa khi tất cả các giá trị được sắp xếp theo thứ tự.

* Để xác định đặc trưng nào phù hợp hơn để đại diện cho mức lương, bạn cần xem xét sự phân bố của dữ liệu:

- Nếu dữ liệu không có giá trị ngoại lệ (outliers), số trung bình sẽ phản ánh mức lương chung.

- Nếu có giá trị ngoại lệ, trung vị sẽ là đặc trưng phù hợp hơn vì nó không bị ảnh hưởng bởi các giá trị cực đoan.

Bạn có thể kiểm tra sự phân bố bằng cách vẽ biểu đồ hộp (boxplot) hoặc kiểm tra sự chênh lệch giữa số trung bình và trung vị. Nếu chênh lệch lớn, có thể có sự hiện diện của giá trị ngoại lệ

Vận dụng Câu 2

Trả lời câu hỏi Vận dụng 2 trang 88 Chuyên đề Tin học 12 Chân trời sáng tạo

Cân nặng (đơn vị: kg) của 20 vận động viên môn cử tạ của một đội tuyển được ghi lại như sau:

Để thuận tiện cho việc luyện tập, huấn luyện viên muốn xếp 20 vận động viên trên thành 4 nhóm, mỗi nhóm gồm 25% số vận động viên có cân nặng gần nhau. Em hãy giúp huấn luyện viên xác định các ngưỡng cân nặng để phân nhóm cho mỗi vận động viên.

Lời giải chi tiết:

Cân nặng (đơn vị: kg) của 20 vận động viên môn cử tạ của một đội tuyển được ghi lại như sau:

Để thuận tiện cho việc luyện tập, huấn luyện viên muốn xếp 20 vận động viên trên thành 4 nhóm, mỗi nhóm gồm 25% số vận động viên có cân nặng gần nhau.

Để phân chia 20 vận động viên thành 4 nhóm theo cân nặng, bạn cần thực hiện các bước sau:

- Sắp xếp cân nặng của vận động viên theo thứ tự tăng dần.

- Tìm giá trị cân nặng tại các phân vị thứ 25%, 50%, và 75% để xác định ngưỡng cho mỗi nhóm.

- Phân chia vận động viên vào các nhóm dựa trên ngưỡng đã tìm được.

Ví dụ, nếu cân nặng của họ sau khi sắp xếp là: 52, 54, 54, 55, 56, 58, 59, 60, 60, 61, 63, 63, 63, 64, 66, 67, 68, 69, 70, 71 kg, thì:

Nhóm 1 (25% thấp nhất): từ 52 đến 56 kg.

Nhóm 2 (25% tiếp theo): từ 58 đến 61 kg.

Nhóm 3 (25% tiếp theo): từ 63 đến 66 kg.

Nhóm 4 (25% cao nhất): từ 67 đến 71 kg.

Những ngưỡng này giúp huấn luyện viên phân nhóm sao cho mỗi nhóm có số lượng vận động viên và cân nặng gần nhau nhất. Điều này sẽ thuận tiện cho việc luyện tập và phát triển kỹ năng cụ thể theo từng nhóm cân nặng.

Vận dụng Câu 3

Trả lời câu hỏi Vận dụng 3 trang 88 Chuyên đề Tin học 12 Chân trời sáng tạo

Trả lời câu hỏi Vận dụng 3 trang 88 Chuyên đề Tin học 12 Chân trời sáng tạo

Em hãy tìm mốt của bảng tần số trên và nêu ý nghĩa của kết quả tìm được.

Lời giải chi tiết:

Khảo sát tiền lương hàng tháng của 30 công nhân của một xưởng may, em có bảng tần số sau:

Dựa vào bảng tần số, mốt của dữ liệu tiền lương hàng tháng là khoản lương có tần số xuất hiện nhiều nhất. Trong trường hợp này, mốt là 9000 đồng với tần số là 6, cao nhất trong bảng.

Ý nghĩa của mốt:

- Mốt (9000 đồng): Đây là mức lương phổ biến nhất mà công nhân của xưởng may nhận được hàng tháng.

- Phản ánh Mức Lương: Mốt cho thấy mức lương mà đa số công nhân trong xưởng may này nhận được, giúp hiểu rõ hơn về điều kiện làm việc và mức sống của họ.

- Quyết Định Chính Sách: Thông tin này có thể được sử dụng để đánh giá và điều chỉnh chính sách tiền lương, cải thiện điều kiện làm việc hoặc hỗ trợ phúc lợi cho công nhân.

Vận dụng Câu 4

Trả lời câu hỏi Vận dụng 4 trang 88 Chuyên đề Tin học 12 Chân trời sáng tạo

Sản lượng lúa (đơn vị: tạ/ha) các năm từ 2014 đến 2018 của hai tỉnh A và B được cho ở bảng sau:

a) Em hãy tính các đặc trưng về độ phân tán của dữ liệu bởi khoảng biến thiên và phương sai của sản lượng lúa từng tỉnh.

b) Tinh nào có sản lượng lúa ổn định hơn? Tại sao?

Lời giải chi tiết:

Sản lượng lúa (đơn vị: tạ/ha) các năm từ 2014 đến 2018 của hai tỉnh A và B được cho ở bảng sau:

Để tính khoảng biến thiên và phương sai của sản lượng lúa từng tỉnh, bạn có thể làm như sau trong Excel:

a) Các bước:

Nhập dữ liệu sản lượng lúa vào bảng tính Excel.

Tính khoảng biến thiên bằng cách lấy giá trị lớn nhất trừ đi giá trị nhỏ nhất trong dữ liệu của mỗi tỉnh.

Tính phương sai bằng công thức =VAR.P(range) trong Excel, với range là phạm vi chứa dữ liệu sản lượng lúa của mỗi tỉnh.

b) Để xác định tỉnh nào có sản lượng lúa ổn định hơn:

So sánh khoảng biến thiên và phương sai của hai tỉnh.

Tỉnh có khoảng biến thiên và phương sai nhỏ hơn cho thấy sản lượng lúa ổn định hơn.

Lưu ý: Cần dữ liệu đầy đủ và chính xác từ tỉnh B để tính toán chính xác, vì hiện tại có vẻ như một số dữ liệu bị che mờ bởi watermark. Nếu không có dữ liệu đầy đủ, không thể đưa ra so sánh chính xác giữa hai tỉnh.

Vận dụng Câu 5

Trả lời câu hỏi Vận dụng 5 trang 88 Chuyên đề Tin học 12 Chân trời sáng tạo

Bảng dưới đây thống kê tổng số giờ nắng trong năm 2020 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở hai tỉnh C và D.

a) Em hãy tính các đặc trưng về độ phân tán của dữ liệu bởi độ lệch chuẩn và hệ số biến thiên của dữ liệu từng tỉnh.

b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh?

Để giải quyết câu hỏi của bạn, bạn cần thực hiện các bước sau trong Excel:

Lời giải chi tiết:

Bảng dưới đây thống kê tổng số giờ nắng trong năm 2020 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở hai tỉnh C và D.

a) Tính độ lệch chuẩn và hệ số biến thiên:

- Độ lệch chuẩn (SD): Sử dụng công thức =STDEV.S(range), thay range bằng dãy ô chứa dữ liệu của từng tỉnh.

- Hệ số biến thiên (CV): Tính bằng cách chia SD cho giá trị trung bình (mean) của dữ liệu, công thức là = (SD / AVERAGE(range)) * 100.

b) Nhận xét về sự thay đổi tổng số giờ nắng:

- Xem xét sự biến đổi của dữ liệu qua các tháng để nhận xét về xu hướng tăng giảm hoặc sự ổn định của tổng số giờ nắng ở mỗi tỉnh.

Lưu ý rằng bạn cần có dữ liệu cụ thể từ bảng để thực hiện các phép tính này. Nếu bạn cần thêm hướng dẫn chi tiết về cách sử dụng Excel, tôi có thể cung cấp thêm thông tin.