Mẫu số liệu ghép nhóm là gì? - Toán 11

Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số của các nhóm số liệu.

+ Mỗi nhóm số liệu là tập hợp gồm các giá trị của số liệu được ghép nhóm theo một tiêu chí xác định, thường được cho dưới dạng [a;b), trong đó a là đầu mút trái, b là đầu mút phải.

+ Độ dài của nhóm [a;b) là b – a.

+ Tần số của một nhóm là số số liệu thuộc vào nhóm đó. Tần số của nhóm 1, nhóm 2,… nhóm m kí hiệu lần lượt là \({n_1}\), \({n_2}\), …, \({n_m}\).

+ Bảng tần số ghép nhóm được lập như bảng dưới đây, trong đó mẫu số liệu gồm n số liệu được chia thành m nhóm tương ứng với m nửa khoảng \(\left[ {{a_1};{a_2}} \right)\); \(\left[ {{a_2};{a_3}} \right)\); …; \(\left[ {{a_m};{a_{m + 1}}} \right)\). Khi đó \({a_1} < {a_2} < ... < {a_m} < {a_{m + 1}}\) và \(n = {n_1} + {n_2} + ... + {n_m}\).

+ Tần số tích luỹ của một nhóm là số số liệu trong mẫu số liệu có giá trị nhỏ hơn giá trị đầu mút phải của nhóm đó. Tần số tích luỹ của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là \(c{f_1}\), \(c{f_2}\), …, \(c{f_m}\). Bảng tần số ghép nhóm bao gồm cả tần số tích luỹ được lập như ở bảng dưới.

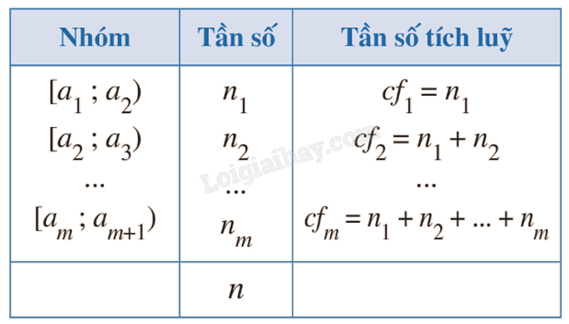
+ Giá trị đại diện của nhóm i là trung điểm \({x_i}\) của nửa khoảng (tính bằng trung bình cộng hai đầu mút) ứng với nhóm i.

Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm được cho dưới dạng bảng tần số ghép nhóm. Hãy cho biết mẫu số liệu đó có bao nhiêu số liệu; bao nhiêu nhóm; tần số của mỗi nhóm.

Giải:

Từ bảng, ta thấy:

- Mẫu số liệu đó gồm 120 số liệu và 5 nhóm.

- Tần số của các nhóm 1, 2, 3, 4, 5 lần lượt là: 11, 31, 45, 21, 12.