Cách tính số trung vị của mẫu số liệu ghép nhóm - Toán 11

Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:

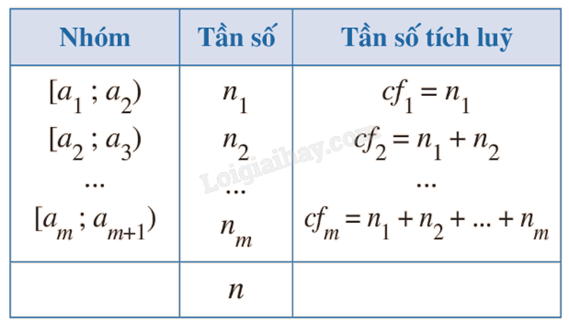
Giả sử k là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{2}\), tức là \(c{f_{k - 1}} < \frac{n}{2}\) nhưng \(c{f_k} \ge \frac{n}{2}\). Ta gọi \(r,d,{n_k}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm k; \(c{f_{k - 1}}\) là tần số tích luỹ của nhóm k – 1.

Trung vị của mẫu số liệu ghép nhóm, kí hiệu \({M_e}\), được tính theo công thức:

\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d\).

Quy ước: \(c{f_0} = 0\).

Trung vị của mẫu số liệu ghép nhóm xấp xỉ cho trung vị của mẫu số liệu gốc, nó chia mẫu số liệu thành hai phần, mỗi phần chứa 50% giá trị.

Sau khi điều tra về số học sinh trong 100 lớp học, người ta chia mẫu số liệu đó thành năm nhóm căn cứ vào số lượng học sinh của mỗi lớp (đơn vị: học sinh) và lập bảng tần số ghép nhóm bao gồm cả tần số tích luỹ như bảng. Tìm trung vị của mẫu số liệu đó (làm tròn kết quả đến hàng đơn vị).

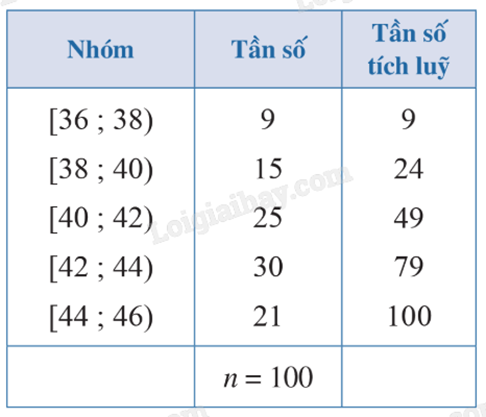
Giải:

Số phần tử của mẫu là n = 100. Ta có: \(\frac{n}{2} = \frac{{100}}{2} = 50\).

Mà 49 < 50 < 79 nên nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng 50.

Xét nhóm 4 là nhóm [42;44) có r = 42, d = 2, \({n_4} = 30\) và nhóm 3 là nhóm [40;42) có \(c{f_3} = 49\).

Áp dụng công thức, ta có trung vị của mẫu số liệu là:

\({M_e} = 42 + \left( {\frac{{\frac{{100}}{2} - 49}}{{30}}} \right).2 \approx 42\) (học sinh).

2) Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tính trung vị của mẫu số liệu ghép nhóm này.

Giải:

Cỡ mẫu: n = 3 + 12 + 15 + 24 + 2 = 56.

Gọi \({x_1},...,{x_{56}}\) là thời gian truy cập Internet của 56 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là \(\frac{{{x_{28}} + {x_{29}}}}{2}\). Do hai giá trị \({x_{28}}\), \({x_{29}}\) thuộc nhóm [15,5;18,5) nên nhóm này chứa trung vị. Ta có:

\({M_e} = 15,5 + \left( {\frac{{\frac{{56}}{2} - 15}}{{15}}} \right).3 = 18,1\).