Cách tính mốt của mẫu số liệu ghép nhóm - Toán 11

Cho mẫu số liệu như bảng dưới.

Giả sử nhóm i là nhóm có tần số lớn nhất. Ta gọi u, g, \({n_i}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm i; \({n_{i - 1}}\), \({n_{i + 1}}\) lần lượt là tần số của nhóm i – 1, nhóm i + 1.

Mốt của mẫu số liệu ghép nhóm, kí hiệu \({M_o}\), được tính theo công thức:

\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g\).

Lưu ý: Người ta chỉ định nghĩa mốt cho mẫu ghép nhóm có độ dài các nhóm bằng nhau. Một mẫu có thể không có mốt hoặc có nhiều hơn một mốt.

Như ta đã biết, một của một mẫu số liệu không ghép nhóm đặc trưng cho số lần lặp lại nhiều nhất tại một giá trị của mẫu số liệu đó. Vì thế, có thể dùng một để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.

Bằng cách ghép nhóm mẫu số liệu và tính toán một của mẫu số liệu ghép nhóm, ta nhận được giá trị môi cũng có thể dùng để đo xu thế trung tâm của mẫu số liệu đã cho.

Một của mẫu số liệu sau khi ghép nhóm xấp xỉ với một của mẫu số liệu không ghép nhóm ban đầu. Một mẫu số liệu ghép nhóm có thể có nhiều một.

1) Kết quả kiếm tra môn Toán của lớp 11D lập thành bảng tần số ghép nhóm như sau:

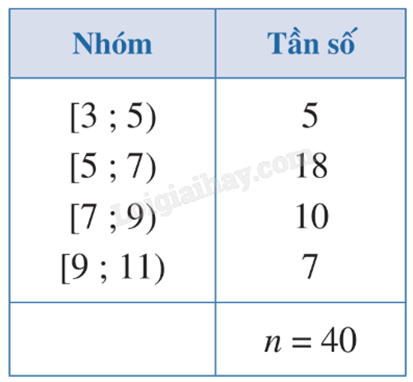
Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu (làm tròn kết quả đến hàng phần mười)?

Giải:

Nhóm 2 ứng với nửa khoảng [5;7) là nhóm có tần số lớn nhất với u = 5; g = 2; \({u_2} = 18\). Nhóm 1 có tần số \({n_1} = 5\), nhóm 3 có tần số \({n_3} = 10\). Áp dụng công thức, ta có mốt của mẫu số liệu là:

\({M_o} = 5 + \left( {\frac{{18 - 5}}{{2.18 - 5 - 10}}} \right).2 \approx 6,2\).

2) Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.

Tính mốt của mẫu số liệu ghép nhóm này. Có thể kết luận gì từ giá trị tính được?

Giải:

Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150;155).

Do đó \({M_o} = 150 + \frac{{14 - 5}}{{(14 - 7) + (14 - 10)}}.5 \approx 153,18\).