Cách tính số trung bình của mẫu số liệu ghép nhóm - Toán 11

Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:

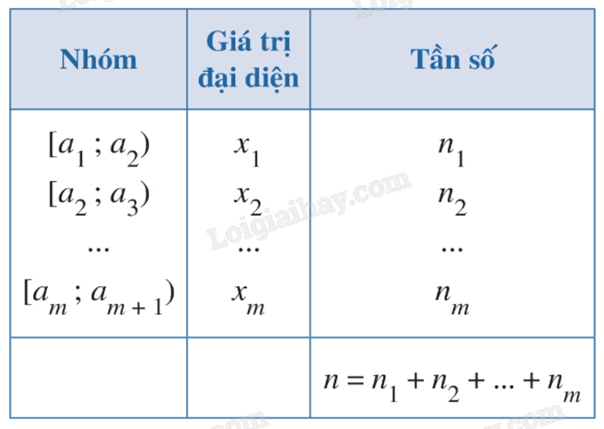
Giá trị đại diện của nhóm i là trung điểm \({x_i}\) của nửa khoảng (tính bằng trung bình cộng hai đầu mút) ứng với nhóm i.

Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau:

\(\overline x  = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}}}{n}\)

trong đó \(n = {n_1} + {n_2} + ... + {n_m}\).

Như ta đã biết, số trung bình cộng của mẫu số liệu không ghép nhóm là giá trị trung bình cộng của các số trong mẫu số liệu đó, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu khi các số liệu trong mẫu ít sai lệch với số trung bình cộng.

Số trung bình cộng của mẫu số liệu sau khi ghép nhóm x̃p xi với số trung bình cộng của mẫu số liệu không ghép nhóm ban đầu và có thể làm đại diện cho vị trí trung tâm của mẫu số liệu.

1) Một nhà thực vật học đo chiều dài của 74 lá cây (đơn vị: milimét) và thu được bằng tần số như bảng.

Tính chiều dài trung bình của 74 lá cây trên theo đơn vị milimét (làm tròn kết quả đến hàng phần trăm).

Giải:

Chiều dài trung bình của 74 lá cây mà nhà thực vật học đo xấp xỉ là:

\(\overline x  = \frac{{5.5,65 + 9.6,05 + 15.6,45 + 19.6,85 + 16.7,25 + 8.7,65 + 2.8,05}}{{74}} \approx 6,80\) (mm).

2) Tìm cân nặng trung bình của học sinh lớp 11D cho trong bảng.

Giải:

Trong mỗi khoảng cân nặng, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:

Tổng số học sinh là n = 42. Cân nặng trung binh của học sinh lớp 11D là:

\(\overline x  = \frac{{10.43 + 7.48 + 16.53 + 4.58 + 2.63 + 3.68}}{{42}} \approx 51,81\) (kg).