Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc (g.c.g)

Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 cạnh và 2 góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ:

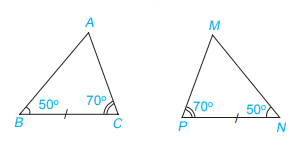
Xét 2 tam giác ABC và MNP có:

\(\begin{array}{l}\widehat B = \widehat N\\BC = NP\\\widehat C = \widehat P\end{array}\)

Vậy \(\Delta ABC = \Delta MNP\)(g.c.g)

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 3 phiếu

Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE