Lý thuyết Xác suất của biến cố - SGK Toán 10 Cánh diều
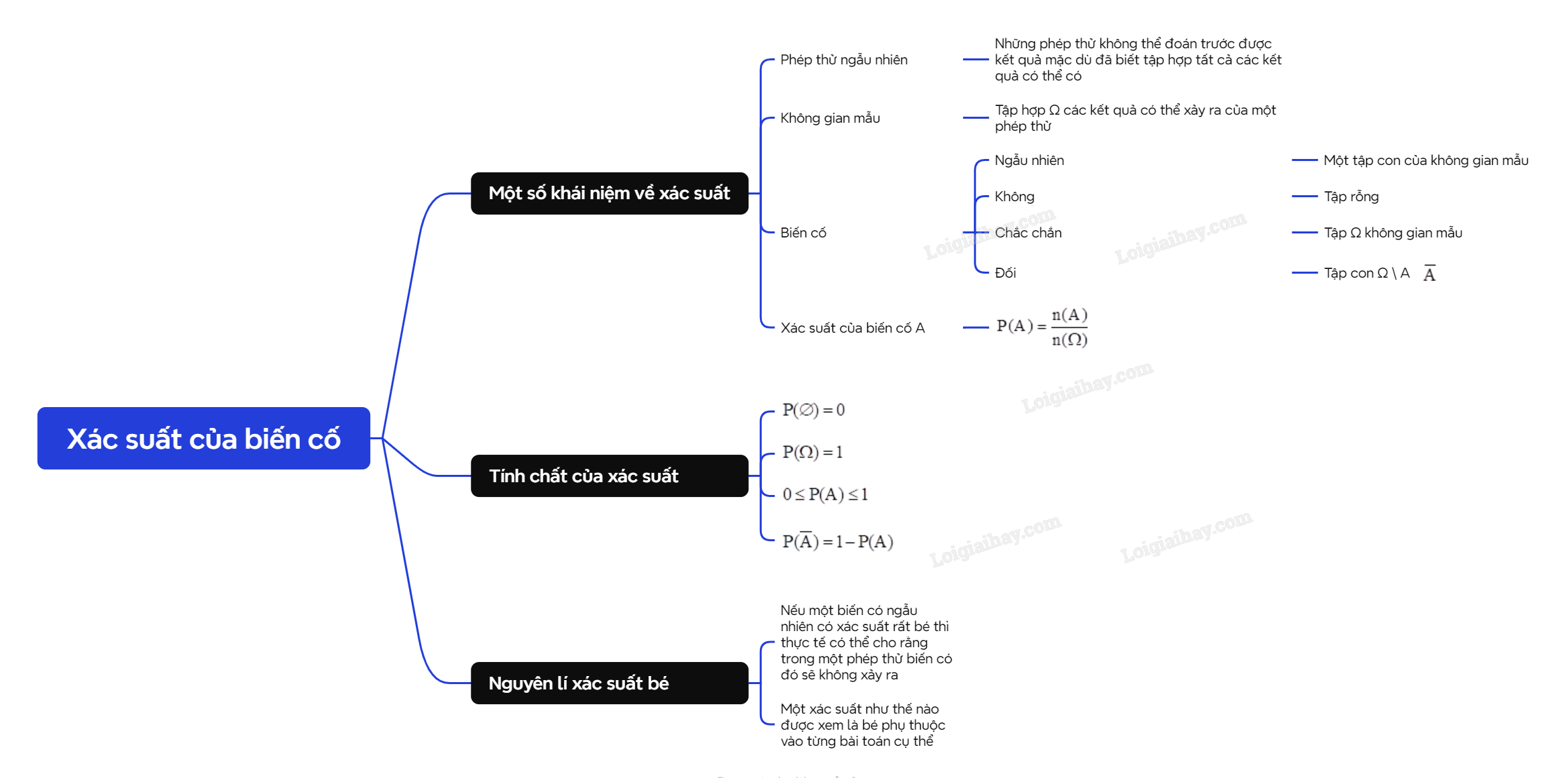
A. Lý thuyết 1. Một số khái niệm về xác suất a) Phép thử ngẫu nhiên và không gian mẫu Một trong những khái niệm cơ bản của lý thuyết xác suất là phép thử. Chẳng hạn, tung đồng xu hay gieo xúc xắc, ... là những ví dụ về phép thử.
A. Lý thuyết
1. Một số khái niệm về xác suất
a) Phép thử ngẫu nhiên và không gian mẫu
Một trong những khái niệm cơ bản của lý thuyết xác suất là phép thử. Chẳng hạn, tung đồng xu hay gieo xúc xắc, ... là những ví dụ về phép thử.
| Có những phép thử mà ta không thể đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó. Những phép thử như thế gọi là phép thử ngẫu nhiên (gọi tắt là phép thử). |
Một cách tổng quát, ta có định nghĩa sau:
| Tập hợp Ω các kết quả có thể xảy ra của một phép thử gọi là không gian mẫu của phép thử đó. |
b) Biến cố
* Biến cố
| Biến cố ngẫu nhiên (gọi tắt là biến cố) là một tập con của không gian mẫu. |
Chú ý: Vì sự kiện chỉ ra tính chất đặc trưng cho các phần tử của một biến cố nên ta cũng gọi biến cố là biến cố. Chẳng hạn: Sự kiện “Kết quả của hai lần tung là giống nhau” trong phép thử “Tung đồng xu hai lần liên tiếp” là một biến cố.
* Biến cố không. Biến cố chắc chắn
| Xét phép thử T với không gian mẫu Ω. Một biến cố là một tập con của tập hợp Ω Vì thế, tập rỗng ∅ cũng là một biến cố, gọi là biến cố không thể (gọi tắt là biến cố không). Còn tập hợp Ω gọi là biến cố chắc chắn. |
* Biến cố đối
| Tập con Ω \ A xác định một biến cố, gọi là biến cố đối của biến cố A, ký hiệu là \(\overline A \). |
Chú ý: Nếu biến cố A được mô tả dưới dạng định nghĩa toán học Q thì biến cố \(\overline A \) được mô tả bằng mệnh đề phủ định của mệnh đề Q (tức là mệnh đề \(\overline Q \)).
c) Xác suất của biến cố
Một cách tổng quát, ta có định nghĩa sau:
Xét phép thử chỉ có một số hữu hạn kết quả có thể xảy ra và khả năng xảy ra của từng kết quả là giống nhau. Gọi Ω là không gian mẫu của phép thử đó. Khi đó, với mỗi biến cố A, ta có định nghĩa cổ điển của xác suất như sau:
| Xác suất của biến cố A, kí hiệu là P(A), bằng tỉ số \(\frac{{n(A)}}{{n(\Omega )}}\), ở đó n(A), n(Ω) lần lượt là số phần tử của hai tập hợp A và Ω. Như vậy: \(P(A) = \frac{{n(A)}}{{n(\Omega )}}\). |
2. Tính chất của xác suất
Xét phép thử T với không gian mẫu Ω.
|
+ \(P(\emptyset ) = 0\); \(P(\Omega ) = 1\). + \(0 \le P(A) \le 1\) với mỗi biến cố A. + \(P(\overline A ) = 1 - P(A)\) với mỗi biến cố A. |
3. Nguyên lí xác suất bé
Nếu một biến có ngẫu nhiên có xác suất rất bé thì thực tế có thể cho rằng trong một phép thử biến có đó sẽ không xảy ra.
Tuy nhiên, một xác suất như thế nào được xem là bé phụ thuộc vào từng bài toán cụ thể.
B. Bài tập
Bài 1: Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên một quả bóng từ trong hộp, ghi lại màu của quả bóng được lấy ra và bỏ lại quả bóng đó vào hộp. Xét phép thử “Lấy ngẫu nhiên tiếp 2 quả bóng trong hộp”. Hãy cho biết không gian mẫu của phép thử đó.
Giải:
Không gian mẫu của phép thử trên là tập hợp Ω = {XX; XD; XV; ĐD; ĐV; DX; DV; VX; VD}, ở đó, chẳng hạn XD là kết quả “Lần thứ nhất lấy ra quả bóng xanh, lần thứ hai lấy ra quả bóng đỏ”.
Bài 2: Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên đồng thời 2 chiếc thẻ từ trong hộp.
a) Gọi Ω là không gian mẫu trong trò chơi trên. Tính số phần tử của tập hợp Ω.
b) Tính xác suất của biến cố E: “Tổng các số trên hai thẻ là số lẻ”.
Giải:
a) Mỗi phần tử của không gian mẫu Ω là một tổ hợp chập 2 của 5 phần tử trong tập hợp {1;2;3;4;5}. Vì thế \(n(\Omega ) = C_5^2 = \frac{{5!}}{{2!.3!}} = \frac{{5.4}}{2} = 10\).
b) Biến cố E gồm các cách chọn ra hai chiếc thẻ ghi số là: 1 và 2; 1 và 4; 2 và 3; 2 và 5; 3 và 4; 4 và 5. Vì thế n(E) = 6. Vậy xác suất của biến cố E là:
\(P(E) = \frac{{n(E)}}{{n(\Omega )}} = \frac{6}{{10}} = \frac{3}{5}\).
Bài 3: Nhân dịp khai trương một cửa hàng kinh doanh đồ điện tử, khách hàng đầu tiên sau khi mua hàng sẽ được nhận một phiếu tặng quà. Món quà là một chiếc tai nghe của một trong năm hãng và tai nghe mỗi hãng có hai màu trắng hoặc đen.
a) Vẽ sơ đồ hình cây biểu thị các khả năng của một món quà mà khách hàng đầu tiên có thể nhận được từ phiếu tặng quà.
b) Tính xác suất của biến cố H: “Khách hàng đầu tiên nhận được chiếc tai nghe màu trắng từ phiếu tặng quà”.
Giải:
a) Sơ đồ hình cây biểu thị các khả năng của một món quà mà khách hàng đầu tiên có thể nhận được từ phiếu tặng quà:

b) Ta thấy không gian mẫu Ω là các loại tai nghe đếm theo hãng và theo màu của tai nghe. Dựa vào sơ đồ hình cây ở trên, ta thấy:
+ n(Ω) = 10.
+ Khách hàng đầu tiên có thể nhận được 1 trong 5 loại tai nghe màu trắng ứng với hãng, tức là n(H) = 5.
Vậy xác suất xảy ra biến cố H là \(P(H) = \frac{{n(H)}}{{n(\Omega )}} = \frac{5}{{10}} = \frac{1}{2}\).
Bài 4: Một hộp có 10 quả bóng trắng và 10 quả bóng đỏ; các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên đồng thời 9 quả bóng trong hộp. Tính xác suất để trong 9 quả bóng được lấy ra có ít nhất một quả bóng màu đỏ.
Giải:
Mỗi cách lấy ra đồng thời 9 quả bóng là một tổ hợp chập 9 của 20 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 9 của 20 phần tử và \(n(\Omega ) = C_{20}^9\).
Xét biến cố K: “Trong 9 quả bóng được lấy ra có ít nhất một quả bóng màu đỏ”.
Khi đó biến cố đối của biến cố K là biến cố \(\overline K \): “Trong 9 quả bóng được lấy ra không có quả bóng màu đỏ nào”, tức là cả 9 quả bóng được lấy ra có màu trắng.
Mỗi cách lấy ra đồng thời 9 quả bóng màu trắng là một tổ hợp chập 9 của 10 phần tử.
Do đó \(n(\overline K ) = C_{10}^9 = \frac{{10!}}{{9!.1!}} = 10\). Suy ra \(P(\overline K ) = \frac{{n(\overline K )}}{{n(\Omega )}} = \frac{{10}}{{C_{20}^9}}\).
Vậy \(P(K) = 1 - P(\overline K ) = 1 - \frac{{10}}{{C_{20}^9}}\).
Các bài khác cùng chuyên mục
- Lý thuyết Ba đường conic - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều
- Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
- Lý thuyết Ba đường conic - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều
- Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều













Danh sách bình luận