-
Toán 8 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 8 tập 2 - Kết nối tri thức
Toán 8, giải toán lớp 8 kết nối tri thức với cuộc sống
Bài 29. Hệ số góc của đường thẳng Toán 8 kết nối tri thức
Lý thuyết Hệ số góc của đường thẳng SGK Toán 8 - Kết nối tri thức
Hệ số góc của đường thẳng là gì?
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
1. Hệ số góc của đường thẳng
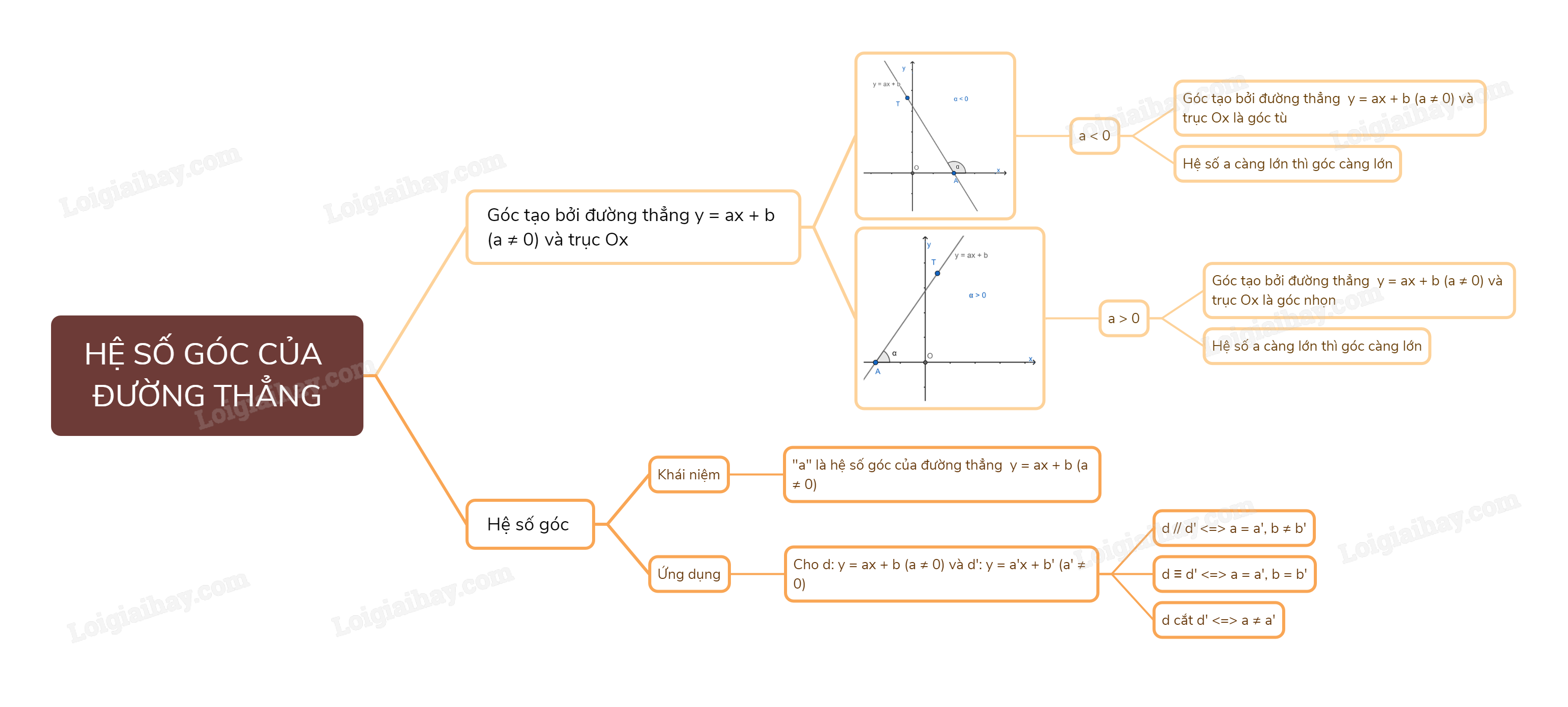
Góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc \(\alpha \) tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc \(\alpha \))
Hệ số góc: Ta gọi a là hệ số góc của đường thẳng y = ax + b (a\( \ne \)0).
Ví dụ: Đường thẳng y = 3x – 1 có hệ số góc là 3;
y = 2 – x có hệ số góc là -1.
2. Nhận biết hai đường thẳng song song
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) song song với nhau khi a = a’; b \( \ne \) b’ và ngược lại.
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) trùng nhau khi a = a’; b = b’ và ngược lại.
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) cắt nhau khi a \( \ne \) a’ và ngược lại.
Ví dụ: Đường thẳng y = -x + 1 và đường thẳng y = -x song song với nhau.
Đường thẳng y = -x + 1 và đường thẳng y = 2x + 1 cắt nhau.
Bình luận
Chia sẻ
- Giải mục 1 trang 51, 52 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải mục 2 trang 53, 54 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 7.30 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 7.31 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 7.32 trang 54 SGK Toán 8 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải dự án 2 trang 112 SGK Toán 8 tập 1
- Lý thuyết Hình chóp tứ giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình chóp tam giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình đồng dạng SGK Toán 8 - Kết nối tri thức
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Kết nối tri thức
