Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá Bài 1. Hàm số y = ax² (a ≠ 0) và đồ thị - Toán 9 Cùng k..

Lý thuyết Hàm số y = ax² (a ≠ 0) và đồ thị Toán 9 Cùng khám phá


1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).

1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).

Ví dụ: Hàm số \(y = 2{x^2},y =  - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).

2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

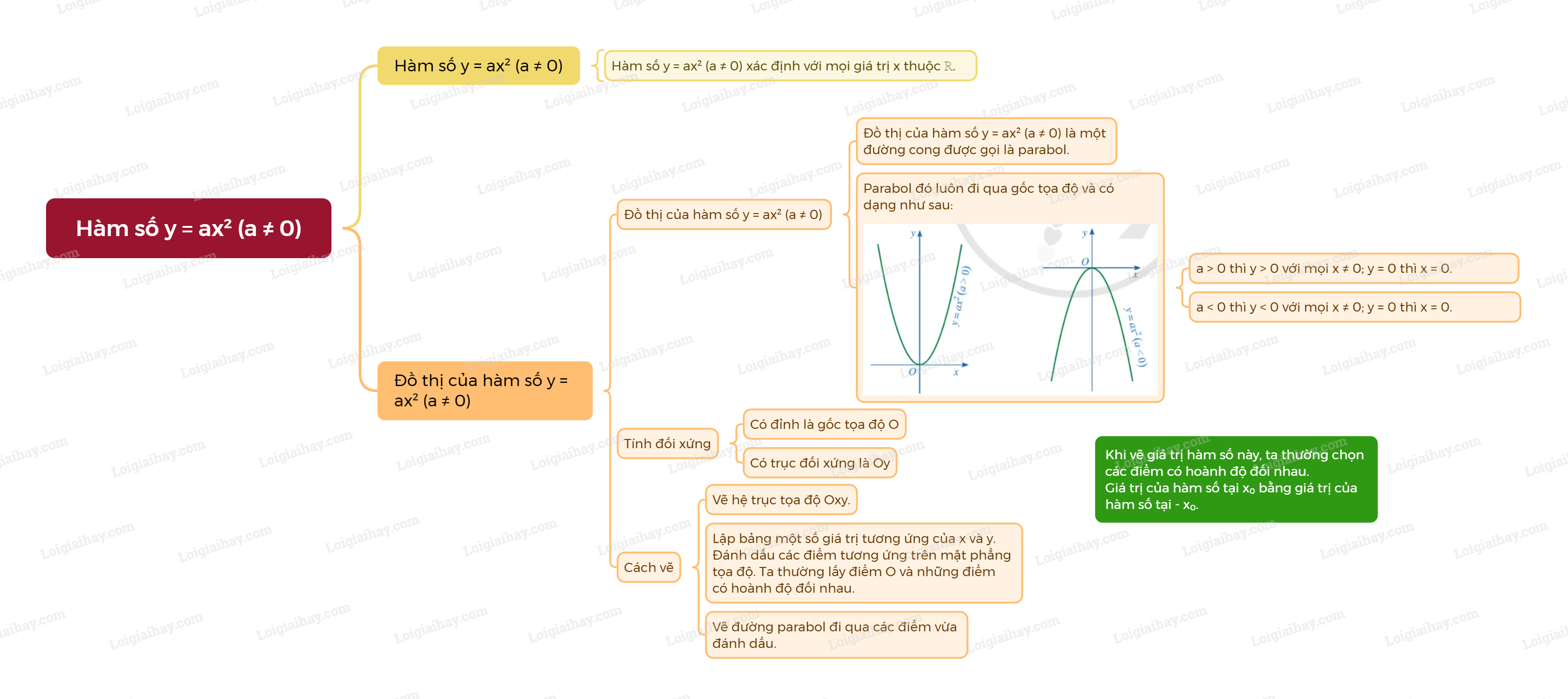
- Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong đi qua gốc tọa độ. Đường cong đó được gọi là một parabol với đỉnh O và nhận trục Oy làm trục đối xứng.

- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

Lưu ý:

- Cho hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).

+ Nếu \(a > 0\) thì \(y > 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\).

+ Nếu \(a < 0\) thì \(y < 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\).

- Vì đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ giá trị của hàm số này, ta thường chọn những điểm có hoành độ đối nhau.

Chỉ cần tính giá trị của hàm số tại \({x_0}\), ta suy ra được giá trị của hàm số tại \( - {x_0}\) vì \(a{\left( { - x{ _0}} \right)^2} = a{x_0}^2\)

Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

- Vẽ hệ trục tọa độ Oxy.

- Lập bảng một số giá trị tương ứng của x và y. Đánh dấu các điểm tương ứng trên mặt phẳng tọa độ. Ta thường lấy điểm O và những điểm có hoành độ đối nhau.

- Vẽ đường parabol đi qua các điểm vừa đánh dấu.

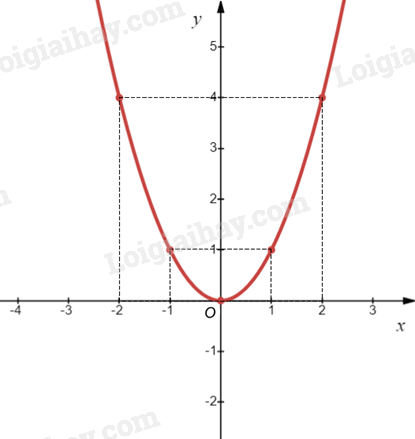
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).

Bảng giá trị của hàm số:

Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store