Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng - Toán 11

Tính chất 1:

- Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

- Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Tính chất 2:

- Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

- Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

1) Cho hình chóp S.ABCD có $SA \perp (ABCD)$, đáy ABCD là hình bình hành có AC cắt BD tại O. Gọi M là trung điểm của SC (Hình 20). Chứng minh rằng $OM \perp (ABCD)$.

Giải:

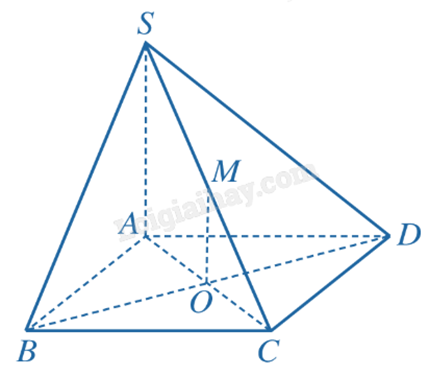
Vì ABCD là hình bình hành nên OA = OC. Ta có OM là đường trung bình của tam giác SAC nên OM // SA. Mà \(SA \bot (ABCD)\) nên \(OM \bot (ABCD)\).

2) Giả sử ABCD và ABMN là hai hình chữ nhật không cùng nằm trong một mặt phẳng. Chứng minh rằng \((ADN)\parallel (BCM)\).

Giải:

Vì hai đường thẳng AD, AN cắt nhau trong mặt phẳng (ADN), \(AB \bot AD\), \(AB \bot AN\) nên \(AB \bot (ADN)\). Do hai đường thẳng BC, BM cắt nhau trong mặt phẳng (BCM), \(AB \bot BC\), \(AB \bot BM\) nên \(AB \bot (BCM)\).

Vì hai mặt phẳng (ADN) và (BCM) cùng vuông góc với AB nên \((ADN)\parallel (BCM)\).