Cách chứng minh hai đường thẳng vuông góc trong không gian - Toán 11

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^o}\).

Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu \(a \bot b\).

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường còn lại.

Cách 1: Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^o}\).

Cách 2: Nếu \(d \bot (P)\) thì d vuông góc với mọi đường thẳng thuộc (P).

Ví dụ minh hoạ:

1) Cho hình hộp ABCD.A'B'C'D' có 6 mặt đều là hình vuông. Chứng minh rằng \(AB \bot CC'\), \(AC \bot B'D'\).

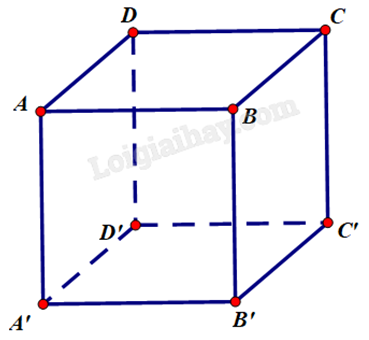
Giải:

Ta có CC' // BB', suy ra \((AB,CC') = (AB,BB') = \widehat {ABB'} = {90^o}\). Vậy \(AB \bot CC'\).

Ta có B'D' // BD, suy ra \((AC,B'D') = (AC,BD) = {90^o}\) (hai đường chéo của hình vuông luôn vuông góc với nhau). Vậy \(AC \bot B'D'\).

2) Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Chứng minh rằng \(AC \bot MN\).

Giải:

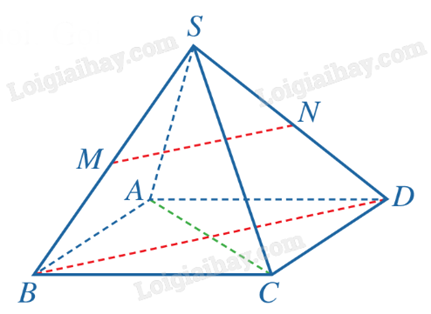
Vì M, N lần lượt là trung điểm của SB và SD nên MN // BD.

Do tứ giác ABCD là hình thoi nên \(AC \bot BD\). Từ các kết quả trên, ta có \(AC \bot MN\).