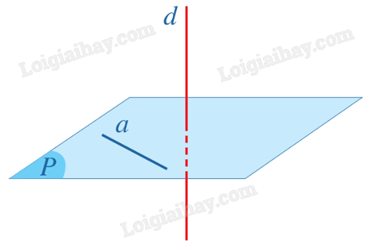
1. Định nghĩa đường thẳng vuông góc với mặt phẳng
Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a trong mặt phẳng (P), kí hiệu \(d \bot (P)\) hoặc \((P) \bot d\).
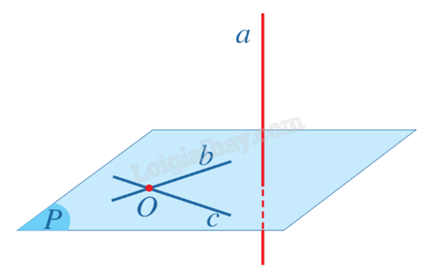
2. Cách chứng minh đường thẳng vuông góc với mặt phẳng
Sử dụng định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Ví dụ minh hoạ:
1) Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và cạnh SA vuông góc với các cạnh AB, AC. Chứng minh rằng \(BC \bot (SAB)\).
Giải:
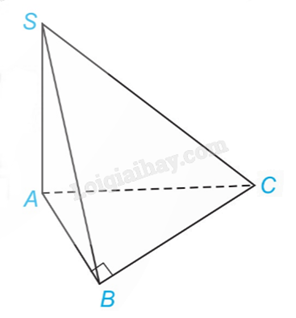
Vì SA vuông góc với hai đường thẳng AB và AC nên \(SA \bot (ABC)\). Suy ra \(SA \bot BC\). Tam giác ABC vuông tại B nên \(BC \bot BA\). Vì BC vuông góc với hai đường thẳng SA và BA nên \(BC \bot (SAB)\).
2) Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SC, SB = SD. Cho I, K lần lượt là trung điểm của các cạnh AB, BC. Chứng minh rằng:
a) \(SO \bot (ABCD)\);
b) \(IK \bot (SBD)\).
Giải:
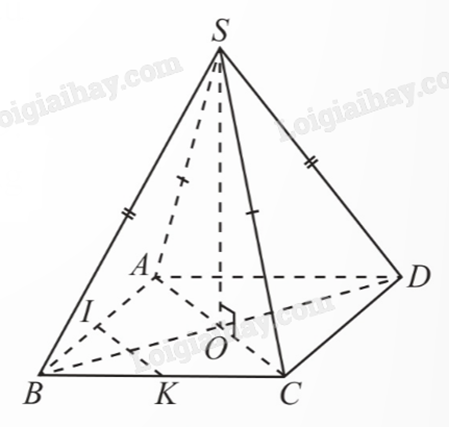
a) Ta có ABCD là hình thoi, suy ra AC, BD vuông góc với nhau và có cùng trung điểm O.
Tam giác SAC cân tại S nên \(SO \bot AC\). Tương tự, ta có \(SO \bot BD\). Do SO vuông góc với hai đường thẳng cắt nhau AC và BD trong (ABCD), suy ra \(SO \bot (ABCD)\).
b) Ta có \(IK\parallel AC\) và \(AC \bot BD\), do đó \(IK \bot BD\).
Ta có \(SO \bot (ABCD)\), do đó \(SO \bot IK\).
Từ \(IK \bot BD\) và \(IK \bot SO\) suy ra \(IK \bot (SBD)\).

 Đường thẳng vuông góc với mặt phẳng - Từ điển môn Toán 11
Đường thẳng vuông góc với mặt phẳng - Từ điển môn Toán 11 






Danh sách bình luận