Giải mục II trang 21, 22, 23, 24 SGK Toán 10 tập 1 - Cánh diều

Hoạt động 2

Trong mặt phẳng toạ độ Oxy, xác định các điểm M(x; y) mà: 

a) $x > 0$ (1); 

b) $y < 1$ (2). 

Lời giải chi tiết:

Để xác định các điểm M(x; y) trong mặt phẳng toạ độ thoả mãn điều kiện đã cho, ta làm như sau: 

a) Đường thẳng $x = 0$ chính là trục tung. 

Đường thẳng $x = 0$ chia mặt phẳng thành hai nửa: nửa mặt phẳng bên trái và nửa mặt phẳng bên phải trục tung. 

Một điểm có hoành độ dương thì nằm ở nửa mặt phẳng bên phải trục tung và ngược lại. Vì thế, miền nghiệm của bất phương trình (1) là nửa mặt phẳng bên phải trục tung, được mô tả bằng nửa mặt phẳng không bị gạch ở Hình 1 (không kể trục tung). 

b) Vẽ đường thẳng $y = 1$. 

Đường thẳng $d: y = 1$ chia mặt phẳng thành hai nửa: nửa mặt phẳng bên trên và nửa mặt phẳng bên dưới đường thẳng $d$ (không kể đường thẳng $d$). 

Một điểm có tung độ nhỏ hơn 1 thì nằm ở nửa mặt phẳng bên dưới đường thẳng $d$ và ngược lại. Vì thế, miền nghiệm của bất phương trình (2) là nửa mặt phẳng bên dưới đường thẳng $d$, được mô tả bằng nửa mặt phẳng không bị gạch ở Hình 2 (không kể đường thẳng $d$).

Hoạt động 3

Cho bất phương trình 2x – y > 2 (3).

a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng \(d:2x - y = 2 \Leftrightarrow y = 2x - 2\).

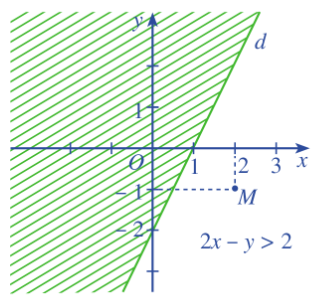
b) Xét điểm M(2;-1). Chứng tỏ (2;-1) là nghiệm của bất phương trình (3).

c) Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2;- 1).

Phương pháp giải:

a) Vẽ đường thẳng y = 2x - 2 trên mặt phẳng tọa độ.

b) Thay tọa độ điểm M vào bất phương trình (3), nếu thỏa mãn thì (2;-1) là một nghiệm của bất phương trình (3).

c) Gạch phần không chứa điểm M.

Lời giải chi tiết:

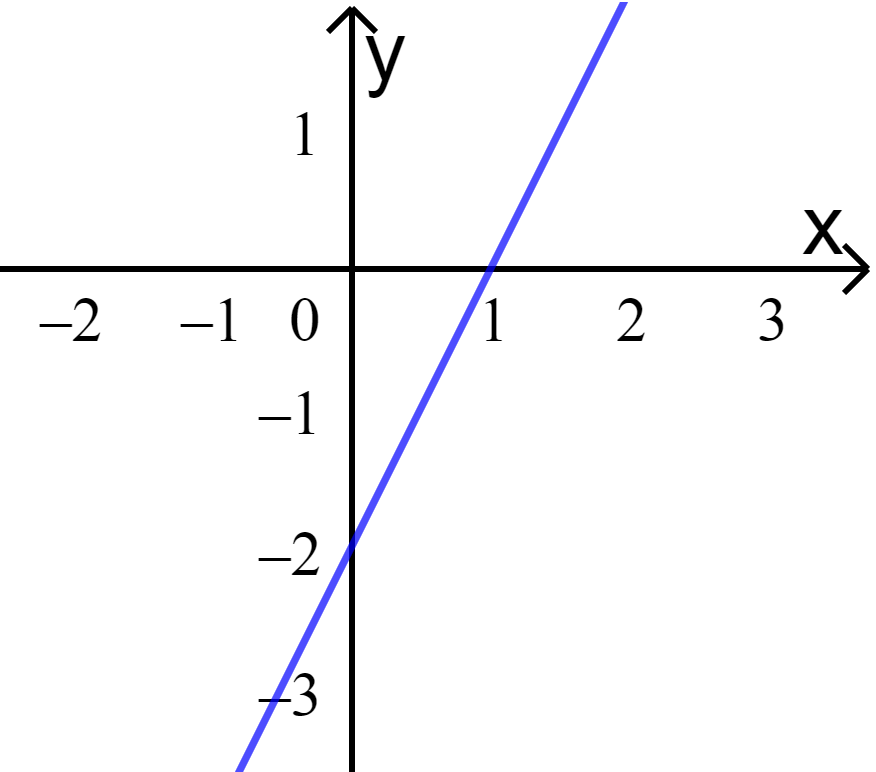
a) Cho x = 0 => y = -2.

Cho y = 0 => x = 1.

Nối hai điểm (0;-2) và (1;0) ta được:

b) Thay tọa độ điểm M vào bất phương trình (3) ta được:

\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)

Vậy (2;-1) là một nghiệm của bất phương trình (3)

c) Ta gạch đi nửa mặt phẳng không chứa M được:

Luyện tập – Vận dụng 2

Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) \(x - 2y < 4\)

b) \(x + 3y \ge 6\).

Phương pháp giải:

Các bước biểu diễn miền nghiệm:

- Vẽ đường thẳng.

- Thay tọa độ điểm O(0;0) vào bất phương trình.

- Nếu thỏa mãn thì điểm O nằm trong miền nghiệm, ta gạch phần không chứa O.

- Ngược lại thì không nằm trong miền nghiệm ta gạch phần chứa O.

Lời giải chi tiết:

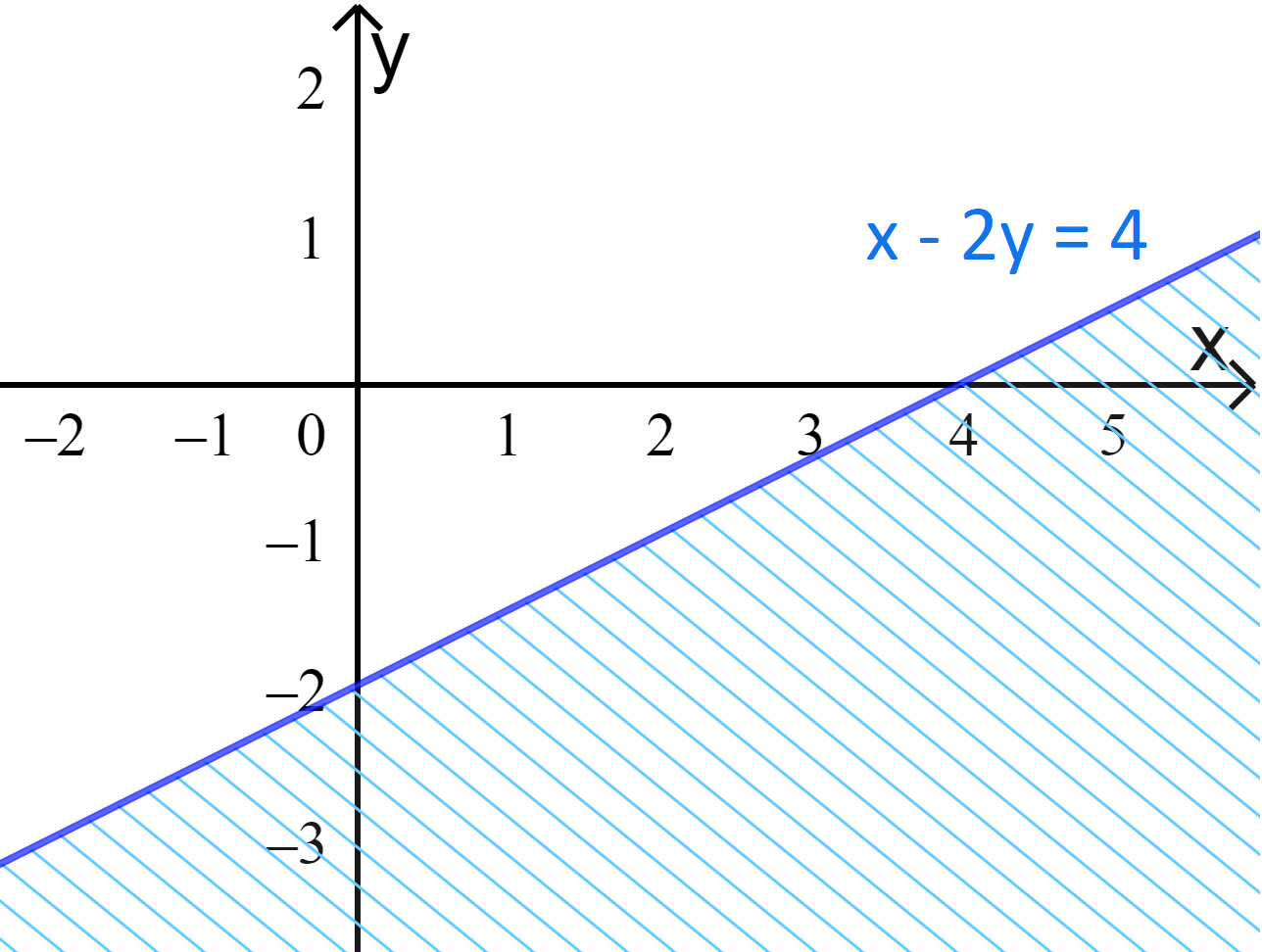
a) Ta vẽ đường thẳng d:\(x - 2y = 4 \Leftrightarrow y = \frac{x}{2} - 2\).

Cho x = 0 thì y = –2, cho y = 0 thì x = 4. Đường thẳng d đi qua 2 điểm (0;–2) và (4;0).

Thay tọa độ điểm O(0;0) vào bất phương trình \(x - 2y < 4\) ta được:

\(0 - 2.0 < 4\) (Luôn đúng).

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

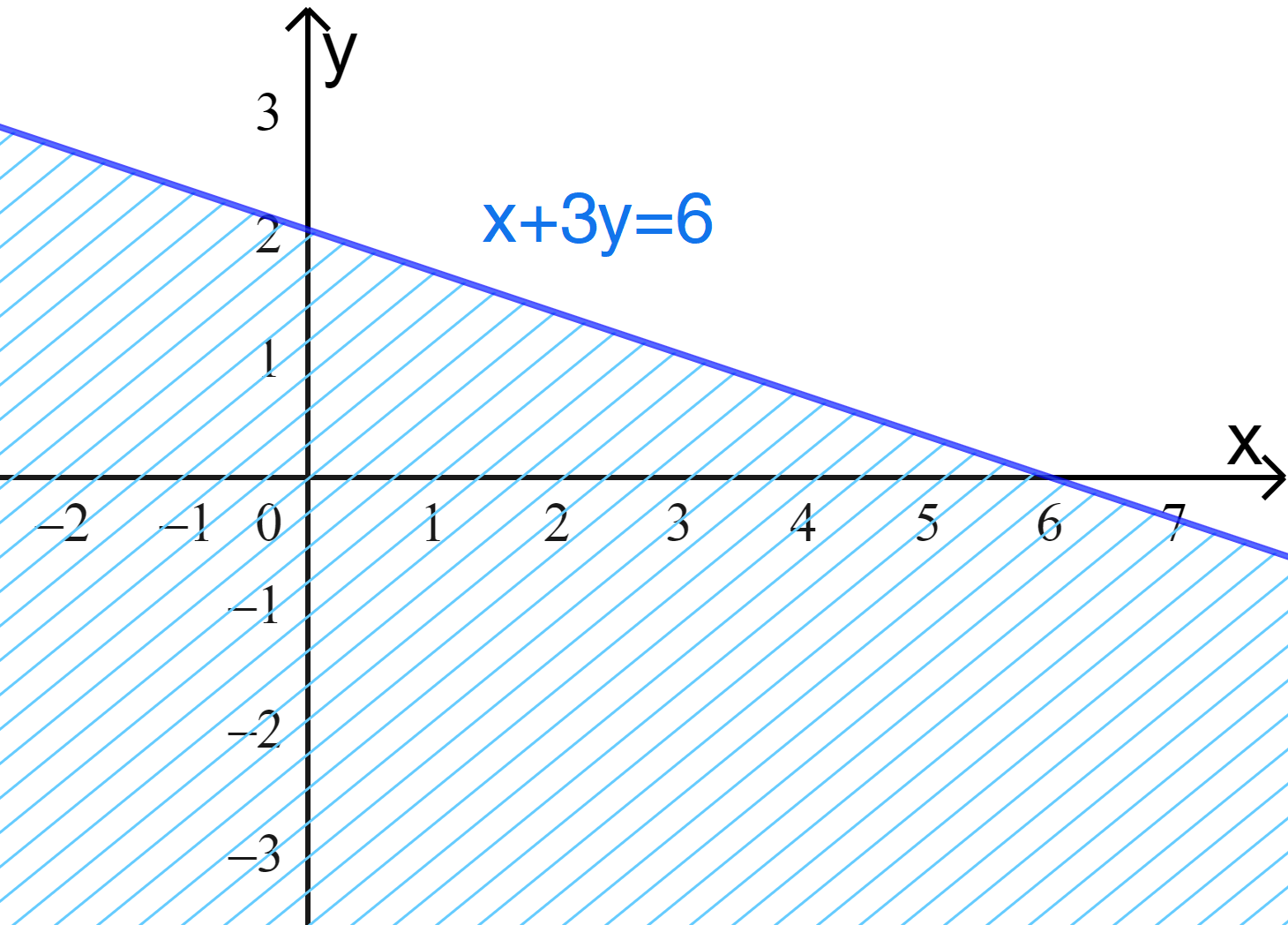
b) Ta vẽ đường thẳng d:\(x+3y=6 \).

Cho x = 0 thì y = 2, cho y = 0 thì x = 6, do đó đường thẳng d đi qua hai điểm (0;2) và (6;0). 

Thay tọa độ điểm O(0;0) vào bất phương trình \(x+3y=6 \) ta được:

\(0+3.0 < 6\).

Vậy O không nằm trong miền nghiệm.

Ta có miền nghiệm: