Giải mục 4 trang 10 SGK Toán 11 tập 2 - Cánh Diều
Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm
HĐ 6
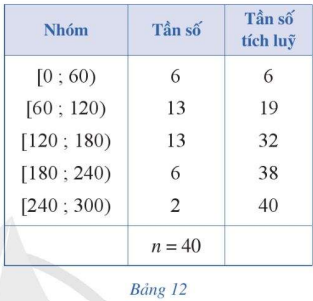
Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm (đơn vị: phút) và lập bảng số ghép nhóm bao gồm cả tần số tích lũy như Bảng 12.
a) Tìm trung vị \({M_e}\) của mẫu số liệu ghép nhóm đó. Trung vị \({M_e}\) còn gọi là tứ phân vị thứ hai \({Q_2}\) của mẫu số liệu trên.
b) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{40}}{4} = 10\) có đúng không?
Tìm đầu mút trái \(s\), độ dài \(h\), tần số \({n_2}\) của nhóm 2; tần số tích lũy \(c{f_1}\) của nhóm 1.
Sau đó, hãy tính giá trị \({Q_1}\) theo công thức sau: \({Q_1} = s + \left( {\frac{{10 - c{f_1}}}{{{n_2}}}} \right).h\).
Giá trị nói trên được gọi là tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đã cho.
c) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\) có đúng không?
Tìm đầu mút trái \(t\), độ dài \(l\), tần số \({n_3}\) của nhóm 3; tần số tích lũy \(c{f_2}\) của nhóm 2.
Sau đó, hãy tính giá trị \({Q_3}\) theo công thức sau: \({Q_3} = t + \left( {\frac{{30 - c{f_2}}}{{{n_3}}}} \right).l\).
Giá trị nói trên được gọi là tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu đã cho.
Phương pháp giải:
Áp dụng các công thức đã được học và công thức được cho để thực hiện bài toán.
Lời giải chi tiết:
a) \({M_e} = 120 + \left( {\frac{{20 - 19}}{{13}}} \right).60 = \frac{{1620}}{{13}}\)
b) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10
- Đầu mút trái của nhóm 2: 60
- Độ dài của nhóm 2: 60
- Tần số của nhóm 2: 13
- Tần số tích lũy của nhóm 1: 6
\({Q_1} = 60 + \left( {\frac{{10 - 6}}{{13}}} \right).60 = \frac{{1020}}{{13}}\)
c) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30
- Đầu mút trái của nhóm 3: 120
- Độ dài của nhóm 3: 60
- Tần số của nhóm 3: 13
- Tần số tích lũy của nhóm 2: 19
\({Q_3} = 120 + \left( {\frac{{20 - 19}}{{13}}} \right).60 = \frac{{1620}}{{13}}\)
LT 6
Tìm tứ phân vị của mẫu số liệu trong Bảng 1.
Phương pháp giải:
Dựa vào kiến thức tứ phân vị vừa làm để xác định.
Lời giải chi tiết:

Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 60
+ Đầu mút trái của nhóm 3: 8
+ Độ dài của nhóm 3: 4
+ Tần số của nhóm 3: 48
+ Tần số tích lũy \(c{f_2}\) của nhóm 2: 42
\({M_e} = 8 + \left( {\frac{{60 - 42}}{{48}}} \right).4 = 9,5\)
Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30
+ Đầu mút trái của nhóm 2: 4
+ Độ dài của nhóm 2: 4
+ Tần số của nhóm 2: 29
+ Tần số tích lũy \(c{f_1}\) của nhóm 1 là: 13
\({Q_1} = 4 + \left( {\frac{{30 - 13}}{{29}}} \right).4 \approx 6,34\)
Nhóm 3 là nhóm đầu tiên có tần số lớn hơn hoặc bằng 90
+ Đầu mút trái của nhóm 3: 8
+ Độ dài của nhóm 3: 4
+ Tần số của nhóm 3: 48
+ Tần số tích lũy \(c{f_2}\) của nhóm 2: 42
\({M_e} = 8 + \left( {\frac{{90 - 42}}{{48}}} \right).4 = 12\)
Các bài khác cùng chuyên mục













Danh sách bình luận