Toán 10, giải toán lớp 10 kết nối tri thức với cuộc sống

Bài 6. Hệ thức lượng trong tam giác Toán 10 Kết nối tri..

Giải mục 2 trang 39, 40 SGK Toán 10 tập 1 - Kết nối tri thức

Trong mỗi hình dưới dây, hãy tính R theo a và sinA. Cho tam giác ABC có b = 8, c = 5 và B=80. Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3
LT2

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 39 SGK Toán 10 Kết nối tri thức

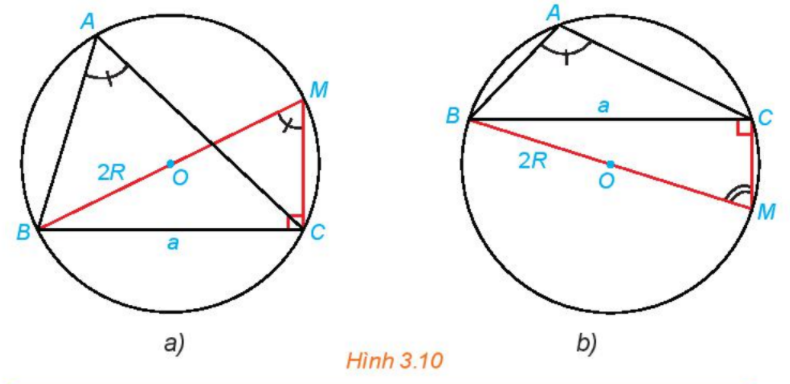
Trong mỗi hình dưới dây, hãy tính R theo a và sinA.

Phương pháp giải:

Bước 1: Tính sin M. Từ đó tính R theo a và sinM.

Bước 2: Tìm mối liên hệ giữa sinA và sinM, suy ra công thức tính R theo sinA.

Lời giải chi tiết:

Xét tam giác MBC vuông tại C ta có:

\(\sin M = \dfrac{{BC}}{{BM}} = \dfrac{a}{{2R}} \Rightarrow R = \dfrac{a}{{2\sin M}}\).

Lại có: Hình 3.10 a: \(\widehat A = \widehat M\) (cùng chắn cung nhỏ BC).

\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)

Hình 3.10b: \(\widehat A + \widehat M = {180^o}\) (cùng tứ giác ABMC nội tiếp đường tròn (O,R)).

\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\).

Vậy ở cả hai hình ta đều có: \(R = \dfrac{a}{{2\sin A}}\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 40 SGK Toán 10 Kết nối tri thức

Cho tam giác ABC có b = 8, c = 5 và \(\widehat B = {80^o}\). Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.

Phương pháp giải:

Bước 1: Tính sin\(\widehat C\), bằng cách áp dụng định lí sin tại đỉnh B và C. Từ đó suy ra số đo góc C.

Bước 2: Tính \(\widehat A\) và suy ra a dựa vào định lí sin.

Bước 3: Tính R.

Lời giải chi tiết:

Áp dụng định lí sin cho tam giác ABC ta có:

\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)

\(\Leftrightarrow \sin C = \frac{{c.\sin B}}{b} = \frac{{5.\sin {{80}^o}}}{8} \approx 0,6155\)

\(\Leftrightarrow \widehat C \approx {38^o}\).

Lại có: \(\widehat A = {180^o} - \widehat B - \widehat C\)

\(= {180^o} - {80^o} - {38^o} = {62^o}\).

Theo định lí sin, ta suy ra:

\(a = \sin A.\dfrac{b}{{\sin B}} = \sin {62^o}\dfrac{8}{{\sin {{80}^o}}} \approx 7,17\).

Và \(2R = \dfrac{b}{{\sin B}} \Rightarrow R = \dfrac{b}{{2\sin B}}\)

\(= \dfrac{8}{{2\sin {{80}^o}}} \approx 4,062\).

Vậy tam giác ABC có \(\widehat A = {62^o}\); \(\widehat C \approx {38^o}\); \(a \approx 7,17\) và \(R \approx 4,062\).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 9 phiếu

Bài tiếp theo

Giải mục 3 trang 40, 41 SGK Toán 10 tập 1 - Kết nối tri thức
Giải tam giác ABC, biết b = 32, c =45, A =87. Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Giải mục 4 trang 41, 42 SGK Toán 10 tập 1 - Kết nối tri thức
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác Cho tam giác ABC với đường cao BD. a) Biểu thị BD theo AB và sinA. Tính diện tích tam giác ABC có b = 2, B = 30, C = 45 Ta đã biết tính cos A theo độ dài các cạnh của tam giác ABC. Liệu sin A và diện tích S có tính theo độ dài các cạnh của tam giác ABC hay không? Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17
Giải bài 3.5 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức
Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.
Giải bài 3.6 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức
Cho tam giác ABC có a = 10, A = 45, B = 70. Tính R,b,c.
Giải bài 3.7 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức
Giải tam giác ABC và tính diện tích của tam giác đó, biết A = 15, B = 130; c = 6.
Giải bài 3.8 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70E với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8 km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo. a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu. b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Giải bài 3.9 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là 50 và 40 so với phương nằm ngang (H.3.18). a) Tính các góc của tam giác ABC. b) Tính chiều cao của tòa nhà.
Giải bài 3.10 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức
Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được).
Giải bài 3.11 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức
Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
Giải mục 1 trang 38, 39 SGK Toán 10 tập 1 - Kết nối tri thức
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b,c và giá trị lượng giác của góc A Định lí Pythagore có phải là một trường hợp đặc biệt của định lí cosin hay không? Từ định lí cosin hãy viết các công thức tính cos A, cos B, cos C Cho tam giác ABC có AB = 5, AC = 8 Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ 1b.
Giải câu hỏi mở đầu trang 38 SGK Toán 10 tập 1 - Kết nối tri thức
Ngắm Tháp Rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí đứng tới tháp rùa. Em có biết vì sao không?
Lý thuyết Hệ thức lượng trong tam giác
1. Định lí cosin 2. Định lí sin 3. Giải tam giác và ứng dụng thực tế