Giải mục 2 trang 16, 17 SGK Toán 10 tập 2 - Chân trời sáng tạo

HĐ Khám phá 2

Lời giải cho phương trình \(\sqrt { - {x^2} + x + 1}  = x\) như sau đúng hai sai?

\(\)\(\sqrt { - {x^2} + x + 1}  = x\)               

\( \Rightarrow  - {x^2} + x + 1 = {x^2}\)  (bình phương cả hai vế để làm mất dấu căn)

\( \Rightarrow  - 2{x^2} + x + 1 = 0\)   (chuyển vế, rút gọn)

\( \Rightarrow x = 1\) hoặc \(x =  - \frac{1}{2}\) (giải phương trình bậc hai)

Vậy phương trình đã cho có hai nghiệm là 1 và \( - \frac{1}{2}\)

Phương pháp giải:

Thay nghiệm tìm được vào phương trình ban đầu ta có:

+) Thay \(x = 1\) vào phương trình \(\sqrt { - {x^2} + x + 1}  = x\) ta thấy thảo mãn phương trình

+) Thay \(x =  - \frac{1}{2}\) vào \(\sqrt { - {x^2} + x + 1}  = x\) ta thấy không thỏa mãn phương trình

Vậy nghiệm của phương trình là \(x = 1\), suy ra lời giải như trên là sai.

Thực hành 2

Giải phương trình \(\sqrt {3{x^2} + 27x - 41}  = 2x + 3\)

Phương pháp giải:

Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 3: Giải phương trình nhận được ở bước 2

Bước 4: Thử lại và kết luận

Lời giải chi tiết:

Bình phương hai vế của phương trình đã cho, ta được:

\(3{x^2} + 27x - 41 = {\left( {2x + 3} \right)^2}\)

\( \Rightarrow 3{x^2} + 27x - 41 = 4{x^2} + 12x + 9\)

\( \Rightarrow {x^2} - 15x + 50 = 0\)

\( \Rightarrow x = 5\) và \(x = 10\)

Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {3{x^2} + 27x - 41}  = 2x + 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy nghiệm của phương trình đã cho là \(x = 5\) và \(x = 10\)

Vận dụng

Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:

a) \(OC = 3OA;\)

b) \(OC = \frac{5}{4}OB\)

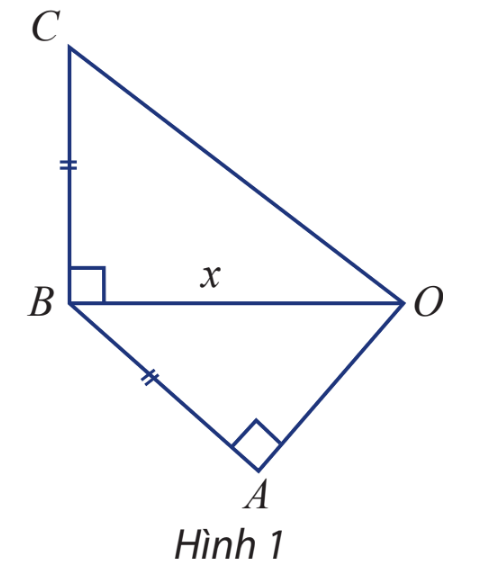
Phương pháp giải:

Bước 1: Sử dụng giả thiết và áp dụng định lý pitago để biểu diễn độ dài OC và OA qua OB

Bước 2: Lập phương trình theo giả thiết \(OC = 3OA;\)\(OC = \frac{5}{4}OB\)

Bước 3: Giải phương trình

Lời giải chi tiết:

Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)

Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)

Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:

\(OC = \sqrt {O{B^2} + B{C^2}}  = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}}  = \sqrt {2{x^2} - 2x + 1} \)

\(OA = \sqrt {O{B^2} - A{B^2}}  = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}}  = \sqrt {2x - 1} \)

a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1}  = 3\sqrt {2x - 1} \)

\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)

\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)

Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1}  = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình

Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)

b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1}  = \frac{5}{4}x\)

\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)

\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)                

Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1}  = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì  \(OC = \frac{5}{4}OB\)