 Toán 10, giải toán lớp 10 chân trời sáng tạo
Toán 10, giải toán lớp 10 chân trời sáng tạo
 Bài 2. Đường thẳng trong mặt phẳng tọa độ Toán 10 Chân..
Bài 2. Đường thẳng trong mặt phẳng tọa độ Toán 10 Chân..
Lý thuyết Đường thẳng trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
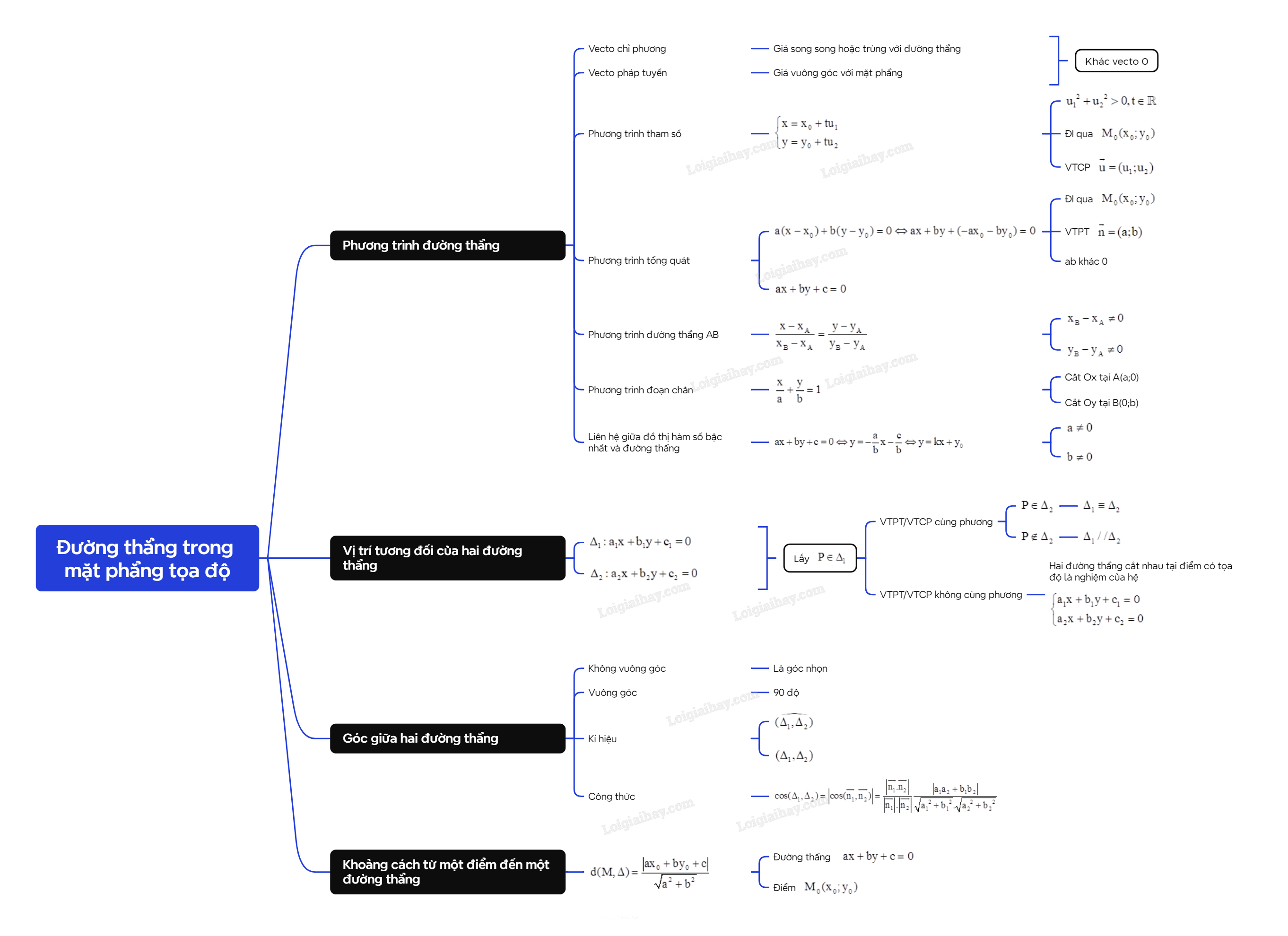
A. Lý thuyết 1. Phương trình đường thẳng a) Vecto chỉ phương và vecto pháp tuyến của đường thẳng
A. Lý thuyết
1. Phương trình đường thẳng
a) Vecto chỉ phương và vecto pháp tuyến của đường thẳng
|
Vecto \(\overrightarrow u \) được gọi là vecto chỉ phương của đường thẳng \(\Delta \) nếu \(\overrightarrow u \ne \overrightarrow 0 \) và giá của vecto \(\overrightarrow u \) song song hoặc trùng với \(\Delta \). Vecto \(\overrightarrow n \) được gọi là vecto pháp tuyến của đường thẳng \(\Delta \) nếu \(\overrightarrow n \ne \overrightarrow 0 \) và giá của vecto \(\overrightarrow n \) vuông góc với \(\Delta \). |
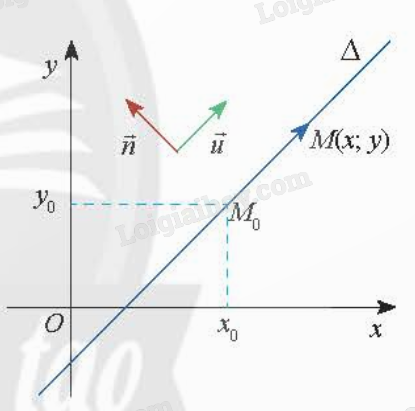
Chú ý:
- Nếu đường thẳng \(\Delta \) có vecto pháp tuyến \(\overrightarrow n = (a;b)\) thì \(\Delta \) sẽ nhận \(\overrightarrow u = (b; - a)\) hoặc \(\overrightarrow u = ( - b;a)\) là một vecto chỉ phương.
- Nếu \(\overrightarrow u \) là một vecto chỉ phương của \(\Delta \) thì \(k\overrightarrow u \) \((k \ne 0)\) cũng là một vecto chỉ phương của \(\Delta \).
- Nếu \(\overrightarrow n \) là một vecto pháp tuyến của \(\Delta \) thì \(k\overrightarrow n \) \((k \ne 0)\) cũng là một vecto pháp tuyến của \(\Delta \).
b) Phương trình tham số của đường thẳng
|
Trong mặt phẳng Oxy, ta gọi \(\left\{ \begin{array}{l}x = {x_0} + t{u_1}\\y = {y_0} + t{u_2}\end{array} \right.\) (với \({u_1}^2 + {u_2}^2 > 0,t \in \mathbb{R}\)) là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow u = ({u_1};{u_2})\) làm vecto chỉ phương. |
Chú ý: Với mỗi giá trị cụ thể của t, ta xác định được một điểm trên đường thẳng \(\Delta \) và ngược lại.
c) Phương trình tổng quát của đường thẳng
|
Trong mặt phẳng Oxy, mỗi đường thẳng đều có phương trình tổng quát dạng \(ax + by + c = 0\) (a và b không đồng thời bằng 0). |
Nhận xét:
- Đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow n = (a;b)\) làm vecto pháp tuyến có phương trình là \(a(x - {x_0}) + b(y - {y_0}) = 0 \Leftrightarrow ax + by + ( - a{x_0} - b{y_0}) = 0\).
- Mỗi phương trình \(ax + by + c = 0\) (a và b không đồng thời bằng 0) đều xác định một đường thẳng \(\Delta \) trong mặt phẳng tọa độ nhận một vecto pháp tuyến là \(\overrightarrow n = (a;b)\).
|
Phương trình đường thẳng \(\Delta \) đi qua hai điểm \(A({x_A};{y_A})\), \(B({x_B};{y_B})\) có dạng \(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}}\) (với \({x_B} - {x_A} \ne 0\) và \({y_B} - {y_A} \ne 0\)). Đường thẳng \(\Delta \) cắt trục Ox, Oy lần lượt tại A(a;0) và B(0;b) có phương trình đoạn chắn là \(\frac{x}{a} + \frac{y}{b} = 1\) \((ab \ne 0)\). |
d) Liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng
- Đường thẳng \(\Delta \) có phương trình tổng quát \(ax + by + c = 0\) (a hoặc b khác 0) là đồ thị hàm số bậc nhất khi và chỉ khi \(a \ne 0\) và \(b \ne 0\). Khi đó, ta có thể viết
\(ax + by + c = 0 \Leftrightarrow y = - \frac{a}{b}x - \frac{c}{b} \Leftrightarrow y = kx + {y_0}\).
- Phương trình trục hoành là y = 0, phương trình trục tung là x = 0.
2. Vị trí tương đối của hai đường thẳng
Trong mặt phẳng Oxy, cho hai đường thẳng \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) \(({a_1}^2 + {b_1}^2 > 0)\) có vecto pháp tuyến \(\overrightarrow {{n_1}} \) và đường thẳng \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(({a_2}^2 + {b_2}^2 > 0)\) có vecto pháp tuyến \(\overrightarrow {{n_2}} \).
|
Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương thì \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau. Lấy một điểm P tùy ý trên \({\Delta _1}\). + Nếu \(P \in {\Delta _2}\) thì \({\Delta _1} \equiv {\Delta _2}\). + Nếu \(P \notin {\Delta _2}\) thì \({\Delta _1}//{\Delta _2}\). Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) không cùng phương thì \({\Delta _1}\) và \({\Delta _2}\) cắt nhau tại một điểm \(M({x_0};{y_0})\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\). |
Chú ý:
a) Nếu \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\) thì \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \), suy ra \({\Delta _1} \bot {\Delta _2}\).
b) Để xét hai vecto \(\overrightarrow {{n_1}} = ({a_1};{b_1})\) và \(\overrightarrow {{n_2}} = ({a_2};{b_2})\) cùng phương hay không, ta xét biểu thức \({a_1}{b_2} - {a_2}{b_1}\):
+ Nếu \({a_1}{b_2} - {a_2}{b_1} = 0\) thì hai vecto cùng phương.
+ Nếu \({a_1}{b_2} - {a_2}{b_1} \ne 0\) thì hai vecto không cùng phương.
Trong trường hợp tất cả các hệ số \({a_1},{a_2},{b_1},{b_2}\) đều khác 0, ta có thể xét hai trường hợp:
+ Nếu \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}}\) thì hai vecto cùng phương.
+ Nếu \(\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}}\) thì hai vecto không cùng phương.
3. Góc giữa hai đường thẳng
a) Khái niệm góc giữa hai đường thẳng
|
Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau tạo thành bốn góc: - Nếu hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) không vuông góc với nhau thì góc nhọn trong bốn góc tạo thành được gọi là góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\). - Nếu hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau thì ta nói góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) bằng \({90^o}\). |
Quy ước:
+ Khi \({\Delta _1}\) song song hoặc trùng với \({\Delta _2}\), ta nói góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) bằng \({0^o}\).
+ Góc giữa hai đường thẳng luôn bé hơn hoặc bằng \({90^o}\), tức là \(({\Delta _1},{\Delta _2}) \le {90^o}\).
+ Góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) được kí hiệu là \((\widehat {{\Delta _1},{\Delta _2}})\) hoặc \(({\Delta _1},{\Delta _2})\).
b) Công thức tính góc giữa hai đường thẳng
|
Trong mặt phẳng tọa độ, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vecto pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = ({a_1};{b_1})\), \(\overrightarrow {{n_2}} = ({a_2};{b_2})\). Ta có: \(\cos ({\Delta _1},{\Delta _2}) = \left| {\cos (\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} )} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}\). |
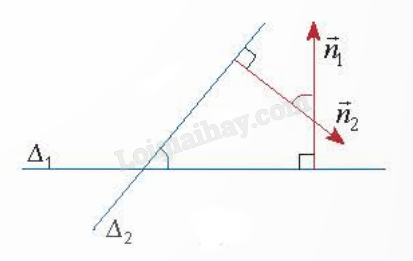
Nhận xét: Nếu \({\Delta _1}\), \({\Delta _2}\) có vecto chỉ phương \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) thì \(\cos ({\Delta _1},{\Delta _2}) = \left| {\cos (\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} )} \right|\).
Chú ý:
+ Nếu \({\Delta _1}\), \({\Delta _2}\) lần lượt có phương trình \({a_1}x + {b_1}y + {c_1} = 0\) và \({a_2}x + {b_2}y + {c_2} = 0\) thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {90^o} \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} = 0\).
+ Nếu \({\Delta _1}\), \({\Delta _2}\) lần lượt có phương trình \(y = {k_1}x + {m_1}\) và \(y = {k_2}x + {m_2}\) thì ta có \(\left( {{\Delta _1},{\Delta _2}} \right) = {90^o} \Leftrightarrow {k_1}{k_2} = - 1\).
Nói cách khác, hai đường thẳng có tích các hệ số góc bằng -1 thì vuông góc với nhau.
4. Khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) có phương trình \(ax + by + c = 0\) \(({a^2} + {b^2} > 0)\) và điểm \({M_0}({x_0};{y_0})\). Khoảng cách từ điểm M đến đường thẳng \(\Delta \), kí hiệu là \(d(M,\Delta )\), được tính bởi công thức sau:
| \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\). |
B. Bài tập
Bài 1:
a) Cho đường thẳng \(\Delta \) có vecto pháp tuyến \(\overrightarrow n = \left( {\frac{1}{2}; - \frac{5}{2}} \right)\). Tìm vecto chỉ phương của \(\Delta \).
b) Cho đường thẳng d có vecto chỉ phương \(\overrightarrow u = (1;3)\). Tìm hai vecto pháp tuyến của d.
Giải:
a) \(\Delta \) có vecto pháp tuyến \(\overrightarrow n = \left( {\frac{1}{2}; - \frac{5}{2}} \right)\), suy ra \(\Delta \) cũng có vecto pháp tuyến \(2\overrightarrow n = \left( {1; - 5} \right)\) và có vecto chỉ phương \(\overrightarrow u = (5;1)\).
b) Hai vecto pháp tuyến của d là \(\overrightarrow n = (3; - 1)\), \( - \overrightarrow n = ( - 3;1)\).
Bài 2: Lập phương trình đường thẳng \(\Delta \) thỏa mãn:
a) Đi qua M(-2;-3) và có \(\overrightarrow n = (2;5)\) là vecto pháp tuyến.
b) Đi qua M(3;-5) và có \(\overrightarrow u = (2; - 4)\) là vecto chỉ phương.
c) Đi qua A(-3;4) và B(1;-1).
Giải:
a) Phương trình \(\Delta \) là \(2(x + 2) + 5(y + 3) = 0 \Leftrightarrow 2x + 5y + 19 = 0\).
b) Phương trình \(\Delta \) là \(\frac{{x - 3}}{2} = \frac{{y + 5}}{{ - 4}} \Leftrightarrow 4x + 2y - 2 = 0 \Leftrightarrow 2x + y - 1 = 0\).
c) Phương trình \(\Delta \) là \(\frac{{x + 3}}{{1 - ( - 3)}} = \frac{{y - 4}}{{ - 1 - 4}} \Leftrightarrow \frac{{x + 3}}{4} = \frac{{y - 4}}{{ - 5}} \Leftrightarrow 5x + 4y - 1 = 0\).
Bài 3: Viết phương trình tổng quát của các đường thẳng là đồ thị hàm số bậc nhất sau:
a) \({d_1}:y = 2x + 3\)
b) \({d_2}:y = - \frac{1}{2}x + 5\)
c) \({d_3}:y = x\)
Giải:
a) Ta có \(y = 2x + 3 \Leftrightarrow 2x - y + 3 = 0\).
Vậy phương trình tổng quát của \({d_1}\) là \(2x - y + 3 = 0\).
b) Ta có \(y = - \frac{1}{2}x + 5 \Leftrightarrow x + 2y - 10 = 0\).
Vậy phương trình tổng quát của \({d_2}\) là \(x + 2y - 10 = 0\).
c) Ta có \(y = x \Leftrightarrow x - y = 0\).
Vậy phương trình tổng quát của \({d_3}\) là \(x - y = 0\).
Bài 4: Xét vị trí tương đối của mỗi cặp đường thẳng sau:
a) \({\Delta _1}:2x - y + 1 = 0\) và \({\Delta _2}: - x + 2y + 2 = 0\).
b) \({\Delta _3}:x - y - 1 = 0\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 2t\end{array} \right.\).
Giải:
a) Đường thẳng \({\Delta _1}\) có vecto chỉ phương \(\overrightarrow {{u_1}} = (1;2)\), đường thẳng \({\Delta _2}\) có vecto chỉ phương \(\overrightarrow {{u_2}} = ( - 2; - 1)\).
Do \(\frac{1}{{ - 2}} \ne \frac{2}{{ - 1}}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương, suy ra \({\Delta _1}\) cắt \({\Delta _2}\).
b) Đường thẳng \({\Delta _3}\), \({\Delta _4}\) lần lượt có vecto chỉ phương là \(\overrightarrow {{u_3}} = (1;1)\) và \(\overrightarrow {{u_4}} = (2;2)\). Suy ra \(\overrightarrow {{u_4}} = 2\overrightarrow {{u_3}} \). Chọn t = 0, ta có điểm \(M(1;3) \in {\Delta _4}\). Do \(1 - 3 - 1 \ne 0\) nên \(M(1;3) \notin {\Delta _3}\).
Vậy \({\Delta _3}\) // \({\Delta _4}\).
Bài 5: Xét vị trí tương đối của hai đường thẳng
\({\Delta _1}:x - 2y + 1 = 0\) và \({\Delta _2}:2x - 4y + 2 = 0\).
Giải:
Tọa độ giao điểm của đường thẳng \({\Delta _1}\) và \({\Delta _2}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 2y + 1 = 0\\2x - 4y + 2 = 0\end{array} \right.\).
Hệ trên có vô số nghiệm. Như vậy, \({\Delta _1}\) và \({\Delta _2}\) có vô số điểm chung, tức hai đường thẳng trên trùng nhau.
Bài 6: Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 {t_1}\\y = 1 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 {t_2}\\y = 4 - {t_2}\end{array} \right.\).
b) \({\Delta _1}:3x + y - 10 = 0\) và \({\Delta _2}: - 2x + y - 7 = 0\).
Giải:
a) \({\Delta _1}\) có vecto chỉ phương \(\overrightarrow {{u_1}} = \left( {\sqrt 3 ;1} \right)\). \({\Delta _2}\) có vecto chỉ phương \(\overrightarrow {{u_2}} = \left( {\sqrt 3 ; - 1} \right)\).
Do đó, ta có: \(\cos ({\Delta _1},{\Delta _2}) = \frac{{\left| {\sqrt 3 .\sqrt 3 + 1.( - 1)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {1^2}} .\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{( - 1)}^2}} }} = \frac{1}{2}\).
Vậy \(({\Delta _1},{\Delta _2}) = {60^o}\).
b) \({\Delta _1}\) có vecto pháp tuyến \(\overrightarrow {{n_1}} = \left( {3;1} \right)\). \({\Delta _2}\) có vecto pháp tuyến \(\overrightarrow {{n_2}} = \left( { - 2;1} \right)\).
Do đó, ta có: \(\cos ({\Delta _1},{\Delta _2}) = \left| {\cos (\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} )} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {3.( - 2) + 1.1} \right|}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{{( - 2)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\).
Vậy \(({\Delta _1},{\Delta _2}) = {45^o}\).
Bài 7: Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) M(-2;1) và \(\Delta :2x - 3y + 5 = 0\).
b) M(1;-3) và \(\Delta :\left\{ \begin{array}{l}x = - 2 + 3t\\y = 2 - 4t\end{array} \right.\).
Giải:
a) Ta có: \(d(M,\Delta ) = \frac{{\left| {2.( - 2) - 3.1 + 5} \right|}}{{\sqrt {{2^2} + {{( - 3)}^2}} }} = \frac{2}{{\sqrt {13} }} = \frac{{2\sqrt {13} }}{{13}}\).
b) Đường thẳng \(\Delta \) đi qua điểm N(-2;2) và có vecto pháp tuyến \(\overrightarrow n = (4;3)\).
Phương trình đường thẳng \(\Delta \) là \(4(x + 2) + 3(y - 2) = 0\). Từ đó, ta nhận được phương trình tổng quát của đường thẳng \(\Delta \) là \(4x + 3y + 2 = 0\).
Vậy \(d(M,\Delta ) = \frac{{\left| {4.1 + 3.( - 3) + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = \frac{3}{5}\).
- Giải mục 1 trang 46, 47, 48, 49, 50, 51 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải mục 2 trang 51, 52, 53 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải mục 3 trang 54, 55, 56, 57 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải mục 4 trang 56, 57 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải bài 1 trang 57 SGK Toán 10 tập 2 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo











