Giải mục 1 trang 97, 98, 99 SGK Toán 12 tập 2 - Cùng khám phá

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cùng khám phá

Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II".

a) Hoàn thành sơ đồ hình cây sau:

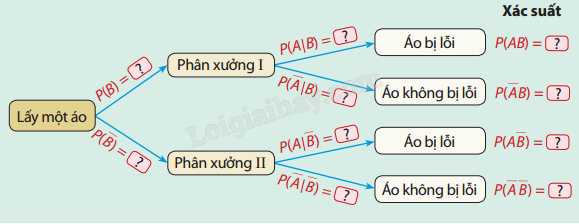
b) Ta nhận thấy biến cố A: "Lấy được áo bị lỗi" có thể xảy ra đồng thời với biến cố B: "Áo được sản xuất bởi phân xưởng I" hoặc biến cố B: "Áo được sản xuất bởi phân xưởng II". Người ta chứng minh được rằng: \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\). Hãy tính xác suất lấy được áo bị lỗi trong lô hàng.

Phương pháp giải:

a) Sử dụng công thức \(P(B|A) = \frac{{P(AB)}}{{P(A)}}\) hoặc \(P(AB) = P(B|A).P(A)\).

b) Sử dụng kết quả ở câu a và áp dụng công thức \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\) để tính xác suất.

Lời giải chi tiết:

a)

- Xác suất phân xưởng I sản xuất áo: \(P(B) = 0,4\)

- Xác suất phân xưởng II sản xuất áo: \(P(\bar B) = 0,6\)

- Xác suất áo bị lỗi từ phân xưởng I: \(P(A|B) = 0,02\)

- Xác suất áo bị lỗi từ phân xưởng II: \(P(A|\bar B) = 0.03\)

- Xác suất áo không bị lỗi từ phân xưởng I và phân xưởng II

Áo không bị lỗi từ phân xưởng I: \(P(\bar A|B) = 1 - P(A|B) \Leftrightarrow P(\bar A|B) = 1 - 0,02 = 0,98\)

Áo không bị lỗi từ phân xưởng II: \(P(\bar A|\bar B) = 1 - P(A|\bar B) \Leftrightarrow P(\bar A|\bar B) = 1 - 0.03 = 0,97\)

- Xác suất \(P(AB)\): Là xác suất áo bị lỗi và thuộc phân xưởng I

\(P(AB) = P(A|B) \cdot P(B) \Leftrightarrow P(AB) = 0,02 \cdot 0,4 = 0,008\)

- Xác suất \(P(\bar AB)\): Là xác suất áo không bị lỗi và thuộc phân xưởng I

\(P(\bar AB) = P(\bar A|B) \cdot P(B) \Leftrightarrow P(\bar AB) = 0,98 \cdot 0,4 = 0,392\)

- Xác suất \(P(A\bar B)\): Là xác suất áo bị lỗi và thuộc phân xưởng II

\(P(A\bar B) = P(A|\bar B) \cdot P(\bar B) \Leftrightarrow P(A\bar B) = 0,03 \cdot 0,6 = 0,018\)     

- Xác suất \(P(\bar A\bar B)\): Là xác suất áo không bị lỗi và thuộc phân xưởng II

\(P(\bar A\bar B) = P(\bar A|\bar B) \cdot P(\bar B) \Leftrightarrow P(\bar A\bar B) = 0,97 \cdot 0,6 = 0,582\)

b)

Xác suất lấy được áo bị lỗi trong lô hàng là:

\(P(A) = P(AB) + P(A\bar B) = 0,008 + 0,018 = 0,026\)

LT1

Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá

Một hộp có 5 quả cầu trắng và 10 quả cầu đen cùng kích thước và khối lượng. Lấy ngẫu nhiên lần lượt hai quả cầu (không hoàn lại) từ hộp. Tính xác suất để lần thứ hai lấy được quả cầu trắng.

Phương pháp giải:

Sử dụng công thức tính xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\).

Lời giải chi tiết:

* Các biến cố:

\(A\): Biến cố lấy quả trắng lần đầu

\(\bar A\): Biến cố lấy quả đen lần đầu

\(B\): Biến cố lấy quả trắng lần thứ hai

Xác suất ban đầu:

\(P(A) = \frac{5}{{15}} = \frac{1}{3}\)

\(P(\bar A) = \frac{{10}}{{15}} = \frac{2}{3}\)

* Xác suất có điều kiện:

\(P(B|A) = \frac{4}{{14}} = \frac{2}{7}\)

\(P(B|\bar A) = \frac{5}{{14}}\)

* Công thức xác suất toàn phần: \(P(B) = P(A) \cdot P(B|A) + P(\bar A) \cdot P(B|\bar A)\)

 Thay số: \(P(B) = \left( {\frac{1}{3} \cdot \frac{2}{7}} \right) + \left( {\frac{2}{3} \cdot \frac{5}{{14}}} \right) = \frac{2}{{21}} + \frac{{10}}{{42}} = \frac{2}{{21}} + \frac{5}{{21}} = \frac{7}{{21}} = \frac{1}{3}\)

 Vậy xác suất lấy được quả cầu trắng lần thứ hai là: \(P(B) = \frac{1}{3}\)

LT2

Trả lời câu hỏi Luyện tập 2 trang 99 SGK Toán 12 Cùng khám phá

Ở một địa phương, tỉ lệ nam và nữ là 2:3. Số người mắc bệnh bạch tạng của địa phương này chiếm tỉ lệ 0,45% dân cư. Tính tỉ lệ nam giới mắc bệnh bạch tạng của địa phương đó, biết tỉ lệ này ở nữ là 0,35%.

Phương pháp giải:

- Sử dụng công thức xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\)

- Xác định tỉ lệ dân số nam và nữ

- Biết tỉ lệ mắc bệnh của từng giới

- Giải phương trình để tìm tỉ lệ nam mắc bệnh

Lời giải chi tiết:

* Xác định các biến cố:

\(A\): Biến cố là nam giới

\(B\): Biến cố là nữ giới

\(C\): Biến cố mắc bệnh bạch tạng

* Theo đề bài ta có các xác suất

\(P(A) = \frac{2}{5}\) ,\(P(B) = \frac{3}{5}\) ,\(P(C) = 0,45\% \) ,\(P(C|B) = 0,35\% \)

* Áp dụng công thức toàn phần

\(P(C) = P(A) \cdot P(C|A) + P(B) \cdot P(C|B)\)

\(0,45\%  = (\frac{2}{5} \cdot P(C|A)) + (\frac{3}{5} \cdot 0,35\% )\)

* Giải Phương Trình

\(0,45\%  = \frac{2}{5} \cdot P(C|A) + 0,21\% \)

\(0,45\%  - 0,21\%  = \frac{2}{5} \cdot P(C|A)\)

\(0,24\%  = \frac{2}{5} \cdot P(C|A)\)

* Tính Tỉ Lệ Nam Mắc Bệnh

\(P(C|A) = \frac{{0,24\%  \cdot 5}}{2}\)

\(P(C|A) = 0,6\% \)

Vậy tỉ lệ nam giới mắc bệnh bạch tạng là \(0,6\% \)