Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống

Bài 14. Phép chiếu song song Toán 11 kết nối tri thức

Giải mục 1 trang 95, 96, 97 SGK Toán 11 tập 1 - Kết nối tri thức

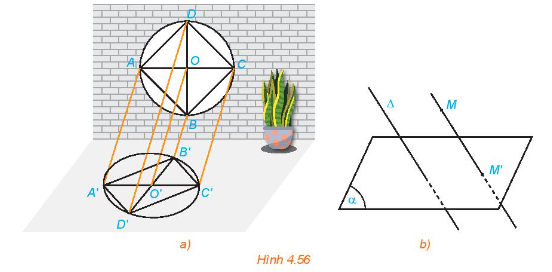
Một khung cửa sổ có dạng hình tròn với các chấn song tạo thành hình vuông ABCD, hai đường chéo của hình vuông cắt nhau tại O. Dưới ánh mặt trời, khung cửa và các chắn song đổ bóng lên sàn nhà (H.4.56a). Quan sát hình vẽ và trả lời các câu hỏi sau: a) Các đường thẳng nối mỗi điểm A, B, C với bóng A’, B’, C’ có đôi một song song hay không? b) Làm thế nào để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ?

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh

Lựa chọn câu để xem lời giải nhanh hơn

HĐ 1

Video hướng dẫn giải

Một khung cửa sổ có dạng hình tròn với các chấn song tạo thành hình vuông ABCD, hai đường chéo của hình vuông cắt nhau tại O. Dưới ánh mặt trời, khung cửa và các chắn song đổ bóng lên sàn nhà (H.4.56a). Quan sát hình vẽ và trả lời các câu hỏi sau:

a) Các đường thẳng nối mỗi điểm A, B, C với bóng A’, B’, C’ có đôi một song song hay không?

b) Làm thế nào để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ?

Phương pháp giải:

Cho mặt phẳng $\left( \alpha \right)$ và đường thẳng cắt $\left( \alpha \right)$. Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:

Nếu M thuộc d thì M’ là giao điểm của $\left( \alpha \right)$ và d.

Nếu M không thuộc d thì M’ là giao điểm của $\left( \alpha \right)$ và đường thẳng qua M song song với d.

Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng $\left( \alpha \right)$ theo phương d.

Lời giải chi tiết:

a) Các đường thẳng nối mỗi điểm A, B, C với bóng A', B', C' có đôi một song song.

b) Để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ ta lấy một đường thẳng a cố định song song với ánh mặt trời.

Điểm O' là giao điểm của sàn nhà và đường thẳng đi qua O song song với a.

Tương tự, ta xác định được các điểm A', B', C', D'.

Video hướng dẫn giải

Trong HĐ1, làm thế nào để xác định được bóng của toàn bộ song cửa CD trên sàn nhà?

Phương pháp giải:

Cho hình $ℜ">R$ , tập hợp các hình chiếu $ℜ'">R'$ của các điểm M thuộc $ℜ">R$ qua phép chiếu song song được gọi là hình chiếu của R qua phép chiếu song song đó.

Lời giải chi tiết:

Để xác định được bóng của toàn bộ song cửa CD, ta xác định bóng của từng điểm C và D trên sàn nhà là C' và D'. Khi đó C'D' chính là bóng của song cửa CD.

LT 1

Video hướng dẫn giải

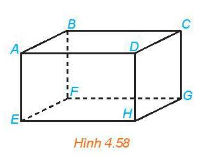
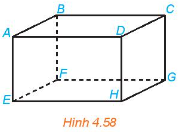
Cho hình hộp ABCD.EFGH (H.4.58). Xác định hình chiếu của điểm A trên mặt phẳng (CDHG) theo phương BC và theo phương BG.

Phương pháp giải:

Cho mặt phẳng $\left( \alpha \right)$ và đường thẳng cắt $\left( \alpha \right)$. Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:

Nếu M thuộc d thì M’ là giao điểm của $\left( \alpha \right)$ và d.

Nếu M không thuộc d thì M’ là giao điểm của $\left( \alpha \right)$ và đường thẳng qua M song song với d.

Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng $\left( \alpha \right)$ theo phương d.

Lời giải chi tiết:

Vì ABCD.EFGH là hình hộp nên BG //AH.

Vì A thuộc mặt phẳng (ABFE) nên H là hình chiếu của A trên mặt phẳng (CDHG) theo phương BG.

VD 1

Video hướng dẫn giải

Trong hình ảnh mở đầu, khi một bàn thắng được ghi thì hình chiếu của quả bóng trên mặt đất theo phương thẳng đứng có vị trí như thế nào với vạch vôi?

Phương pháp giải:

Dựa vào phương pháp tìm hình chiếu của 1 điểm theo phương song song.

Lời giải chi tiết:

Khi một bàn thắng được ghi thì hình chiếu của quả bóng trên mặt đất theo phương thẳng đứng nằm phía trong vạch vôi cùng bờ với khung thành.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 2 trang 97, 98 SGK Toán 11 tập 1 - Kết nối tri thức
Quan sát Hình 4.56a và trả lời các câu hỏi sau: a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không? b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau? c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay
Giải mục 3 trang 98, 99 SGK Toán 11 tập 1 - Kết nối tri thức
Trong ba hình dưới đây, hình nào thể hiên hình lập phương chính xác hơn?
Bài 4.29 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức
Những mệnh đề nào trong các mệnh đề sau đây là đúng? a) Phép chiếu song song biến đoạn thẳng thành đoạn thẳng b) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng cắt nhau c) Phép chiếu song song biến tam giác đều thành tam giác cân d) Phép chiếu song song biến hình vuông thành hình bình hành.
Bài 4.30 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức
Nếu tam giác A’B’C’ là hình chiếu của tam giác ABC qua một phép chiếu song song thì tam giác ABC có phải là hình chiếu của tam giác A’B’C’ qua một phép chiếu song song hay không? Giải thích vì sao.
Bài 4.31 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức
Phép chiếu song song biến tam giác ABC thành tam giác A’B’C’. Chứng minh rằng phép chiếu đó biến trọng tâm của tam giác ABC thành trọng tâm của tam giác A’B’C’.
Bài 4.32 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức
Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?
Bài 4.33 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức
Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình thang, AB song song với CD và AB = 2cm, CD = 6cm.
Bài 4.34 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức
Trong hình bên, AB và CD là bóng của hai thanh chắn của một chiếc thang dưới ánh mặt trời. Hãy giải thích tại sao AB song song với CD
Lý thuyết Phép chiếu song song - SGK Toán 11 Kết nối tri thức
1. Phép chiếu song song