-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá
Bài 2. Một số hệ thức về cạnh và góc của tam giác vuông..
Giải mục 1 trang 83, 84 SGK Toán 9 tập 1 - Cùng khám phá
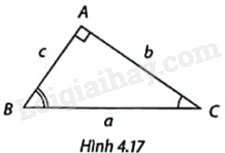
Cho \(\Delta ABC\) vuông tại A như Hình 4.17. Xác định tên các góc nhọn ở các ô ?: Vì \(\frac{b}{a} = \cos ?\) nên \(b = a.\cos ?\); Vì \(\frac{b}{a} = \sin ?\) nên \(b = a.\sin ?\); Vì \(\frac{b}{c} = \tan ?\) nên \(b = c.\tan ?\); Vì \(\frac{b}{c} = \cot ?\) nên \(b = c.\cot ?\);
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 83 SGK Toán 9 Cùng khám phá
Cho \(\Delta ABC\) vuông tại A như Hình 4.17. Xác định tên các góc nhọn ở các ô ?:
Vì \(\frac{b}{a} = \cos ?\) nên \(b = a.\cos ?\);
Vì \(\frac{b}{a} = \sin ?\) nên \(b = a.\sin ?\);
Vì \(\frac{b}{c} = \tan ?\) nên \(b = c.\tan ?\);
Vì \(\frac{b}{c} = \cot ?\) nên \(b = c.\cot ?\);
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Vì \(\frac{b}{a} = \cos C\) nên \(b = a.\cos C\);
Vì \(\frac{b}{a} = \sin B\) nên \(b = a.\sin B\);
Vì \(\frac{b}{c} = \tan B\) nên \(b = c.\tan B\);
Vì \(\frac{b}{c} = \cot C\) nên \(b = c.\cot C\);
LT1
Trả lời câu hỏi Luyện tập 1 trang 84 SGK Toán 9 Cùng khám phá
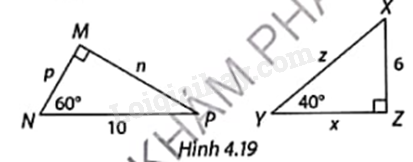
Tính các độ dài n, p, x, z trong Hình 4.19. Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
\(\Delta \)MNP vuông tại M nên
\(p = NP\cos N = 10\cos {60^o} = 10.\frac{1}{2} = 5\),
\(n = NP\sin N = 10\sin {60^o} = 10.\frac{{\sqrt 3 }}{2} \approx 8,66\)
Tam giác XYZ vuông tại Z nên
\(x = 6\cot {40^o} \approx 7,15\), \(z = \frac{6}{{\sin {{40}^o}}} \approx 9,33\).
VD1
Trả lời câu hỏi Vận dụng 1 trang 84 SGK Toán 9 Cùng khám phá
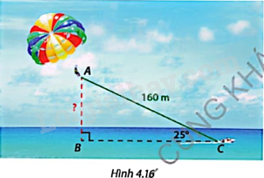
Quay lại bài toán ở phần Khởi động. Góc tạo bởi dây kéo dù bay và phương ngang là \(\widehat {ACB} = {25^o}\).
a) Tính độ cao AB của dù bay nếu dây kéo AC dài 160m.
b) Nếu muốn bay cao 75m thì dây kéo phải dài bao nhiêu mét?
Làm tròn kết quả đến hàng phần mười mét.
Bài toán khởi động: Ca nô dù bay là một trò chơi thể thao biển được ưa chuộng, trong đó người chơi được đeo dù và được ca nô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao như Hình 4.17.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
a) Tam giác ABC vuông tại B nên
\(AB = AC.\sin C = 160.\sin {25^o} \approx 67,6\left( m \right)\)
b) Ta có: \(AB = 75m\).
Tam giác ABC vuông tại B nên \(AB = AC.\sin C\) suy ra \(AC = \frac{{AB}}{{\sin C}} = \frac{{75}}{{\sin {{25}^o}}} \approx 177,5\left( m \right)\).
Bình luận
Chia sẻ
- Giải mục 2 trang 84, 85 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 4.7 trang 86 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 4.8 trang 86 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 4.9 trang 86 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 4.10 trang 86 SGK Toán 9 tập 1 - Cùng khám phá
>> Xem thêm
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
