Bài 1. Đơn thức và đa thức nhiều biến Toán 8 chân trời ..

Giải mục 1 trang 7 SGK Toán 8 tập 1– Chân trời sáng tạo

Cho các biểu thức sau:

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 1

Video hướng dẫn giải

Một số biểu thức được phân chia thành các nhóm như dưới đây:

a) Các biểu thức ở nhóm A có đặc điểm gì phân biệt với các biểu thức ở nhóm B và nhóm C?

b) Các biểu thức ở nhóm A và nhóm B có đặc điểm gì chung, phân biệt với các biểu thức ở nhóm C?

Phương pháp giải:

- Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến

- Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Lời giải chi tiết:

a) Các biểu thức ở nhóm A là các biểu thức đại số chỉ gồm một số, hoặc một tích giữa các số và các biến.

Các biểu thức ở nhóm B và nhóm C là tổng, hiệu hoặc thương của các biểu thức đại số gồm một số, hoặc một tích giữa các số và các biến.

b) Các biểu thức ở nhóm A và nhóm B chỉ gồm tổng, hiệu hoặc tích giữa các số và các biến.

Các biểu thức ở nhóm C có xuất hiện phép chia giữa các biến hoặc phép toán lấy căn bậc hai số học của biến.

Thực hành 1

Video hướng dẫn giải

Cho các biểu thức sau:

\(ab - \pi {r^2}\); \(\dfrac{{4\pi {r^3}}}{3}\); \(\dfrac{p}{{2\pi }}\); \(x - \dfrac{1}{y}\); \(0\); \(\dfrac{1}{{\sqrt 2 }}\); \({x^3} - x + 1\).

Trong các biểu thức trên, hãy chỉ ra:

a) Các đơn thức;

b) Các đa thức và số hạng tử của chúng

Phương pháp giải:

a) Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến

b) Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Lời giải chi tiết:

a) Các đơn thức là: \(\dfrac{{4\pi {r^3}}}{3}\); \(\dfrac{p}{{2\pi }}\); \(0\); \(\dfrac{1}{{\sqrt 2 }}\).

b) Các đa thức là: \(ab - \pi {r^2}\); \({x^3} - x + 1\).

Đa thức \(ab - \pi {r^2}\) có hai hạng tử.

Đa thức \({x^3} - x + 1\) có ba hạng tử

Vận dụng 1

Video hướng dẫn giải

Một bức tường hình thang có cửa sổ hình tròn với các kích thước như hình 1 (tính bằng m).

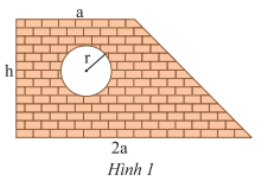
a) Viết biểu thức biểu thị diện tích bức tường (không tính phần cửa sổ).

b) Tính giá trị diện tích trên khi \(a = 2\)m; \(h = 3m\), \(r = 0,5\)m (lấy \(\pi = 3,14\); làm tròn kết quả đến hàng trăm).

Phương pháp giải:

Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).

Lời giải chi tiết:

a) Diện tích bức tường (có tính cửa sổ) là: \(\dfrac{{\left( {a + 2a} \right).h}}{2} = \dfrac{{3ah}}{2} = \dfrac{3}{2}ah\).

Diện tích cửa sổ là: \(r.r.3,14 = 3,14{r^2}\)

Biểu thức biểu thị diện tích bức tường (không tính cửa sổ) là: \(S = \dfrac{3}{2}ah - 3,14{r^2}\)

b) Thay \(a = 2\)m; \(h = 3m\), \(r = 0,5\)m vào đa thức \(S\) ta có:

\(S = \dfrac{3}{2}.2.3 - 3,14.0,{5^2} = 9 - 0,785 = 8,215 \approx 8,22\)

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 17 phiếu

Bài tiếp theo

Giải mục 2 trang 8 SGK Toán 8 tập 1– Chân trời sáng tạo
Để tính thể tích của hình hộp chữ nhật ở hình 2, bạn An viết (V = 3xy.2x), còn bạn Tâm viết (V = 6{x^2}y). Nêu nhận xét về kết quả của hai bạn
Giải mục 3 trang 9 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3. a) Tính tổng thể tích của hình hộp chữ nhật A và B. b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Giải mục 4 trang 10, 11 SGK Toán 8 tập 1 – Chân trời sáng tạo
Cho hai đa thức (A = 5{x^2} - 4xy + 2x - 4{x^2} + xy); (B = {x^2} - 3xy + 2x). Tính giá trị của (A) và (B) tại (x = - 2); (y = dfrac{1}{3}). So sánh hai kết quả nhận được.
Giải Bài 1 trang 11 SGK Toán 8 tập 1 – Chân trời sáng tạo
Chỉ ra các đơn thức, đa thức trong các biểu thức sau:
Giải Bài 2 trang 11 SGK Toán 8 tập 1 – Chân trời sáng tạo
Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.
Giải Bài 3 trang 11 SGK Toán 8 tập 1 – Chân trời sáng tạo
Thu gọn và tìm bậc của mỗi đa thức sau:
Giải Bài 4 trang 11 SGK Toán 8 tập 1 – Chân trời sáng tạo
Tính giá trị của đa thức
Giải Bài 5 trang 11 SGK Toán 8 tập 1 – Chân trời sáng tạo
Viết biểu thức biểu thị thể tích (V) và diện tích xung quanh (S) của hình hộp chữ nhật trong Hình (5). Tính giá trị của (V), (S) khi (x = 4)cm; (y = 2)cm và (z = 1)cm.
Lý thuyết Đơn thức và đa thức nhiều biến SGK Toán 8 - Chân trời sáng tạo
1. Đơn thức