 Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
 Bài 13. Mở đầu về đường tròn trang 97, 98, 99 Vở thực h..
Bài 13. Mở đầu về đường tròn trang 97, 98, 99 Vở thực h..
Giải câu hỏi trắc nghiệm trang 97, 98 vở thực hành Toán 9
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là A. trung điểm của BC. B. trung điểm của AC. C. trung điểm của AB. D. trọng tâm của tam giác ABC.
Chọn phương án đúng trong mỗi câu sau:
Câu 1
Trả lời Câu 1 trang 97 Vở thực hành Toán 9
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là
A. trung điểm của BC.
B. trung điểm của AC.
C. trung điểm của AB.
D. trọng tâm của tam giác ABC.
Phương pháp giải:
+ Gọi O là trung điểm của BC.
+ Chứng minh \(OA = OB = OC\), suy ra O là tâm đường tròn đi qua ba đỉnh của tam giác ABC.
Lời giải chi tiết:
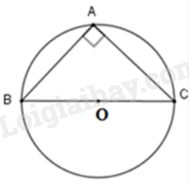
Gọi O là trung điểm của BC.
Tam giác ABC vuông tại A, có AO là đường trung tuyến nên \(OA = OB = OC\). Do đó, O là tâm đường tròn đi qua ba đỉnh của tam giác ABC.
Vậy tâm đường tròn đi qua ba đỉnh của tam giác ABC vuông tại A là trung điểm của BC.
Chọn A
Câu 2
Trả lời Câu 2 trang 97 Vở thực hành Toán 9
Trên mặt phẳng tọa độ Oxy, cho các điểm A(-1; -1), B(-1; -2), C\(\left( {\sqrt 2 ;\sqrt 2 } \right)\) và đường tròn tâm O bán kính 2cm. Khẳng định nào sau đây là sai?
A. Điểm A nằm trong đường tròn (O; 2).
B. Điểm B nằm trên đường tròn (O; 2).
C. Điểm C nằm trên đường tròn (O; 2).
D. Điểm B nằm ngoài đường tròn (O; 2).
Phương pháp giải:
Biểu diễn các điểm và đường tròn (O) trên mặt phẳng tọa độ rồi tìm đáp án đúng.
Lời giải chi tiết:
Biểu diễn các điểm và đường tròn (O) trên mặt phẳng tọa độ ta có:
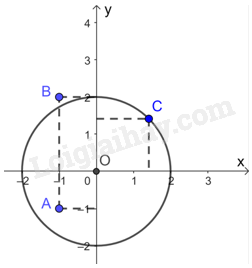
Nhìn vào hình vẽ ta thấy, điểm B nằm ngoài đường tròn (O; 2), điểm A nằm trong đường tròn (O; 2), điểm C nằm trên đường tròn (O; 2).
Chọn B
Câu 3
Trả lời Câu 3 trang 98 Vở thực hành Toán 9
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Khẳng định nào sau đây là đúng?
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn.
B. Bốn điểm A, E, H, D cùng nằm trên một đường tròn.
C. \(DE < BC\).
D. Cả ba đáp án trên đều đúng.
Phương pháp giải:
+ Gọi G, K lần lượt là trung điểm của AH, BC.
+ Chứng minh \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
+ Chứng minh \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
+ Sử dụng quan hệ giữa cạnh và góc trong tam giác chứng minh được \(DE < BC\).
Lời giải chi tiết:
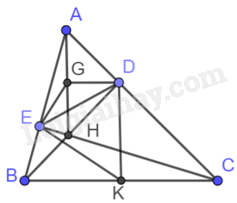
Gọi G, K lần lượt là trung điểm của AH, BC.
Vì EG là đường trung tuyến trong tam giác AEH vuông tại E nên \(EG = GH = AG\).
Vì DG là đường trung tuyến trong tam giác ADH vuông tại D nên \(DG = GH = AG\).
Do đó \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
Vì EK là đường trung tuyến trong tam giác BEC vuông tại E nên \(EK = BK = KC\).
Vì DK là đường trung tuyến trong tam giác BDC vuông tại D nên \(DK = BK = KC\).
Do đó \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
Tam giác EDC có góc EDC là góc tù nên \(ED < EC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Tam giác BEC vuông tại E nên \(EC < BC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Do đó, \(DE < BC\)
Chọn D
Câu 4
Trả lời Câu 4 trang 98 Vở thực hành Toán 9
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng là đường kính.
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng là đường kính.
Phương pháp giải:
Đường tròn có vô số trục đối xứng là đường kính.
Lời giải chi tiết:
Đường tròn có vô số trục đối xứng là đường kính.
Chọn D
- Giải bài 1 trang 98 vở thực hành Toán 9
- Giải bài 2 trang 98 vở thực hành Toán 9
- Giải bài 3 trang 99 vở thực hành Toán 9
- Giải bài 4 trang 99 vở thực hành Toán 9
- Giải bài 5 trang 100 vở thực hành Toán 9
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay











