Giải câu hỏi mở đầu trang 28 SGK Toán 12 tập 1 - Cánh diều

Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức \(Q(t) = - \frac{1}{5}{t^3} + 5{t^2} + 100\), trong đó Q được tính theo \({m^3}\)/phút, t tính theo phút, \(0 \le t \le 20\) (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 \({m^3}\)/phút thì cảnh báo lũ được đưa ra. Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức

\(Q(t) = - \frac{1}{5}{t^3} + 5{t^2} + 100\),

trong đó Q được tính theo \({m^3}\)/phút, t tính theo phút, \(0 \le t \le 20\) (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 \({m^3}\)/phút thì cảnh báo lũ được đưa ra. Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?

Phương pháp giải - Xem chi tiết

Tìm t sao cho \(Q(t) \ge 550\).

Quảng cáo

Lời giải chi tiết

Xét hàm số \(Q(t) = - \frac{1}{5}{t^3} + 5{t^2} + 100\) với \(t \in [0;20]\).

Ta có \(Q'(t) = - \frac{3}{5}{t^2} + 10t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \frac{{50}}{3}\end{array} \right.\)

Bảng biến thiên:

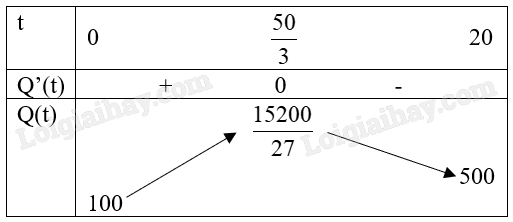
Từ bảng biến thiên suy ra giá trị lớn nhất của lưu lượng nước là \(\frac{{15200}}{{27}}\) \({m^3}\)/phút tại thời điểm \(t = \frac{{50}}{3}\) phút.

Cảnh báo lũ được đưa ra khi lưu lượng nước của con sông lên đến 550 \({m^3}\)/phút, khi đó:

\(Q(t) \ge 550 \Leftrightarrow - \frac{1}{5}{t^3} + 5{t^2} + 100 \ge 550 \Leftrightarrow - \frac{1}{5}{t^3} + 5{t^2} - 450 \ge 0\)

\( \Leftrightarrow \left[ \begin{array}{l}t \le 5 - 5\sqrt 7 \\15 \le t \le 5 + 5\sqrt 7 \end{array} \right.\)

Mà \(t \in [0;20]\) nên \(15 \le t \le 5 + 5\sqrt 7 \).

Vậy tại thời điểm \(t \in \left[ {15;5 + 5\sqrt 7 } \right]\) phút thì cảnh báo lũ được đưa ra.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi trang 28 SGK Toán 12 tập 1 - Cánh diều
Sơ đồ khảo sát hàm số
Giải bài tập 1 trang 42 SGK Toán 12 tập 1 - Cánh diều
đồ thị hàm số \(y = {x^3} - 3x - 1\) là đường cong sau ?
Giải bài tập 2 trang 42 SGK Toán 12 tập 1 - Cánh diều
đường cong ở hình 29 là đồ thị của hàm số :
Giải bài tập 3 trang 43 SGK Toán 12 tập 1 - Cánh diều
Đường cong nào sau đây là đò thị của hàm số (y = frac{{1 - x}}{{x + 1}}) ?
Giải bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh diều
Đường cong ở hình 30 là đồ thị của hàm số:
Giải bài tập 5 trang 43 SGK Toán 12 tập 1 - Cánh diều
khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau: (a,;y = 2{x^3} - 3x + 1 b,;y = - {x^3} + 3x - 1) c, ( y = {left( {x - 2} right)^3} + 4) d,(y = - {x^3} + 3{x^2} - 1) e, (y = frac{1}{3}{x^3} + {x^2} + 2x + 1) g,( y = - {x^3} - 3x)
Giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
Khảo sát sự biến thiên của các hàm số sau: a, \(y = \frac{{x - 1}}{{x + 1}}\) b,\(y = \frac{{ - 2x}}{{x + 1}}\) c,\(y=\frac{{{x^2} - 3x + 6}}{{x - 1}}\) d,\(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\) e,\(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\) g,\(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)
Giải bài tập 7 trang 44 SGK Toán 12 tập 1 - Cánh diều
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm độ cao hát của con tàu so với bề mặt của mặt trăng được tính gần đúng bởi hàm. (hleft( t right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250) Trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét a) Vẽ đồ thị của hàm số (y = hleft( t right)) với (0{rm{ }} le t le {rm{ }
Giải bài tập 8 trang 44 SGK Toán 12 tập 1 - Cánh diều
Xét phản ứng hoá học tạo ra chất C từ hai chất A và B: \(A{\rm{ }} + {\rm{ }}B{\rm{ }} \to {\rm{ }}C\) Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức: \(\left[ C \right]\; = \;\frac{{{a^2}Kt}}{{aKt + 1}}\) (mol/l), trong đó K là hằng số dương. a) Tìm tốc độ phản ứng ở thời điểm t > 0. b) Chứng minh nếu \(x\; = \;\left[ C \right]\) thì c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t\; \to \
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 Cánh Diều
1. Sơ đồ khảo sát hàm số Các bước khảo sát hàm số