Giải câu hỏi mở đầu trang 20 SGK Toán 12 tập 1 - Kết nối tri thức

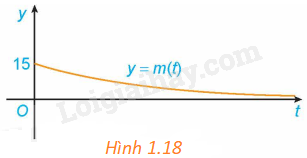
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số (mleft( t right) = 15{e^{ - 0,012t}}). Khối lượng m(t) thay đổi ra sao khi (t to + infty )? Điều này thể hiện trên Hình 1.18 như thế nào?

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).

Quảng cáo

Lời giải chi tiết

Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\).

Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).

Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 20, 21 SGK Toán 12 tập 1 - Kết nối tri thức
Đường tiệm cận ngang
Giải mục 2 trang 21, 22 SGK Toán 12 tập 1 - Kết nối tri thức
Đường tiệm cận đứng
Giải mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức
Đường tiệm cận xiên
Giải bài tập 1.16 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Hình 1.26 là đồ thị của hàm số (y = fleft( x right) = frac{{2{x^2}}}{{{x^2} - 1}}) Sử dụng đồ thị này, hãy: a) Viết kết quả của các giới hạn sau: (mathop {lim }limits_{x to - infty } fleft( x right)); (mathop {lim }limits_{x to + infty } fleft( x right)); (mathop {lim }limits_{x to {1^ - }} fleft( x right)); (mathop {lim }limits_{x to - {1^ + }} fleft( x right)) b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Giải bài tập 1.17 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Đường thẳng \(x = 1\) có phải là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\) không?
Giải bài tập 1.18 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm các tiệm cận của đồ thị hàm số sau: a) \(y = \frac{{3 - x}}{{2x + 1}}\); b) \(y = \frac{{2{x^2} + x - 1}}{{x + 2}}\).
Giải bài tập 1.19 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là \(C\left( x \right) = 2x + 50\) (triệu đồng). Khi đó, \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Tính chất này nói lên điều gì?
Giải bài tập 1.20 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức
Một mảnh vườn hình chữ nhật có diện tích bằng \(144{m^2}\). Biết độ dài một cạnh của mảnh vườn là x (m). a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn. b) Tìm các tiệm cận của đồ thị hàm số P(x).
Lý thuyết Đường tiệm cận của đồ thị hàm số Toán 12 Kết nối tri thức
1. Đường tiệm cận ngang