-
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
-
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Giải bài 8 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau
Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau
Lời giải chi tiết
Gọi AH, BK, CI là đường cao của tam giác ABC kẻ từ đỉnh A, B, C
GH’, GK’, GI’ là đường cao của tam giác GBC, GAC, GAB kẻ từ G xuống BC, AC, AB
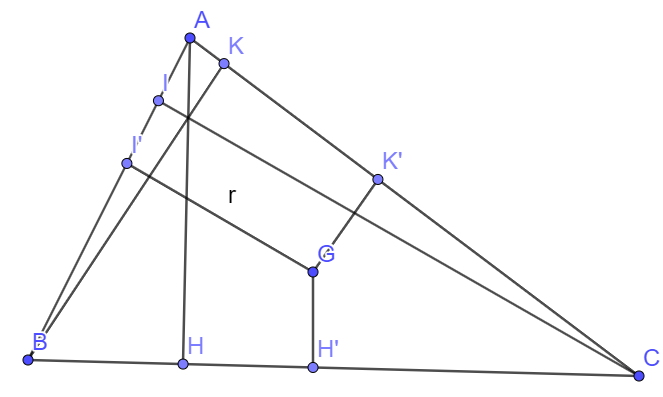
Ta có:
\({S_{GBC}} = \frac{1}{2}BC.GH';{S_{GAC}} = \frac{1}{2}AC.GK';{S_{GBA}} = \frac{1}{2}BA.GI'\)
Mà G là trọng tâm của tam giác ABC nên \(GH' = \frac{1}{3}AH;GK' = \frac{1}{3}BK;GI' = \frac{1}{3}CI\)
Suy ra \({S_{GBC}} = \frac{1}{6}BC.AH;{S_{GAC}} = \frac{1}{6}AC.BK;{S_{GBA}} = \frac{1}{6}BA.CI\) (1)
Mặt khác ta có \({S_{ABC}} = \frac{1}{2}BC.AH = \frac{1}{2}AB.CI = \frac{1}{2}AC.BK\) (2)
Từ (1) và (2) ta có \({S_{GBC}} = {S_{GAB}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\) (đpcm)
Bình luận
Chia sẻ
- Giải bài 9 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 10 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 7 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 6 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 5 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí
