Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2

Bài 7. Vị trí tương đối của hai đường tròn

Bài 70 trang 168 SBT toán 9 tập 1

Giải bài 70 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A...

Đề bài

Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Dây \(AC\) của đường tròn \((O)\) tiếp xúc với đường tròn \((O’)\) tại \(A.\) Dây \(AD\) của đường tròn \((O’)\) tiếp xúc với đường tròn \((O)\) tại \(A.\) Gọi \(K\) là điểm đối xứng với \(A\) qua trung điểm \(I\) của \(OO’,\) \(E\) là điểm đối xứng với \(A\) qua \(B.\) Chứng minh rằng:

\(a)\) \(AB ⊥ KB;\)

\(b)\) Bốn điểm \(A, C, E, D\) nằm trên cùng một đường tròn.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức:

+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là trung trực của dây chung.

+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

+) Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó

+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Để chứng minh các điểm cùng thuộc một đường tròn, ta chứng minh chúng cùng cách đều một điểm.

Lời giải chi tiết

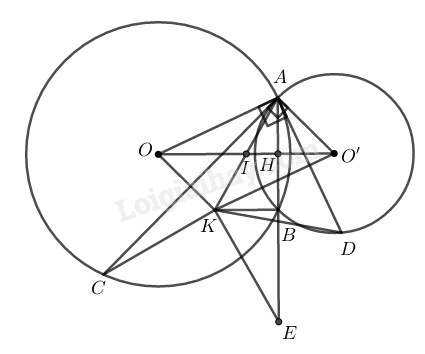
\(a)\) Gọi \(H\) là giao điểm của \(AB\) và \(OO’.\)

Vì hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B\) nên \(OO’\) là đường trung trực của \(AB\)

Hay \(OO’ ⊥ AB\) tại \(H\) và \(HA = HB\)

Lại có \(I\) là trung điểm của \(OO’\) nên \(IH ⊥ AB\;\; (1)\)

Trong tam giác \(ABK,\) ta có:

\(HA = HB\) (chứng minh trên)

\(IA = IK\) (tính chất đối xứng tâm)

Suy ra \(IH\) là đường trung bình của tam giác \(ABK\)

Suy ra \(IH // BK \;\; (2)\)

Từ \((1)\) và \((2)\) suy ra: \(AB ⊥KB\)

\(b)\) Vì \(AB ⊥ KB\) nên \(AE ⊥ KB\)

Lại có: \(AB = BE\) ( tính chất đối xứng tâm)

Suy ra KB là đường trung trực của AE

Do đó: \(KA = KE\) ( tính chất đường trung trực) \((3)\)

Ta có: \(IO = IO’\;\; (gt)\)

\(IA = IK \) ( chứng minh trên)

Tứ giác \(AOKO’\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

Suy ra: \(OK // O’A\) và \(OA // O’K\)

\(CA ⊥ O’A \) (vì \(CA\) là tiếp tuyến của đường tròn \((O’)\))

\(OK // O’A\) ( chứng minh trên)

Suy ra: \(OK ⊥ AC\)

Xét đường tròn (O) có \(OK ⊥ AC\) mà OK là 1 phần đường kính và AC là dây cung nên OK đi qua trung điểm của AC.

Khi đó \(OK\) là đường trung trực của \(AC\)

Suy ra: \(KA = KC\) ( tính chất đường trung trực) \((4)\)

\(DA ⊥ OA\) ( vì \(DA\) là tiếp tuyến của đường tròn \((O)\))

\(O’K // OA\) ( chứng minh trên)

Suy ra: \(O’K ⊥ DA\)

Xét đường tròn (O') có \(O'K ⊥ DA\) mà O'K là 1 phần đường kính và AD là dây cung nên O'K đi qua trung điểm của AD.

Khi đó \(O’K\) là đường trung trực của \(AD\)

Suy ra: \(KA = KD\) ( tính chất đường trung trực) \((5)\)

Từ \((3),\) \((4)\) và \((5)\) suy ra: \(KA = KC = KE = KD\)

Vậy bốn điểm \(A, C, E, D\) cùng nằm trên một đường tròn.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 9 phiếu

Bài tiếp theo

Bài 7.1 phần bài tập bổ sung trang 168 SBT toán 9 tập 1
Giải bài 7.1 phần bài tập bổ sung trang 168 sách bài tập toán 9. Cho h.bs.23, trong đó OA = 3, O'A = 2, AB = 5. Độ dài AC bằng:...
Bài 7.2 phần bài tập bổ sung trang 168 SBT toán 9 tập 1
Giải bài 7.2 phần bài tập bổ sung trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Một đường thẳng vuông góc với AB tại B cắt các đường tròn (O) và (O) theo thứ tự tại C và D ( khác B)...
Bài 69 trang 168 SBT toán 9 tập 1
Giải bài 69 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O)...
Bài 68 trang 168 SBT toán 9 tập 1
Giải bài 68 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD.
Bài 67 trang 167 SBT toán 9 tập 1
Giải bài 67 trang 167 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD.
Bài 66 trang 167 SBT toán 9 tập 1
Giải bài 66 trang 167 sách bài tập toán 9. Cho hai đường tròn (O), (O’) tiếp xúc nhau tại A như trên hình 78. Chứng minh rằng các bán kính OB và O’C song song với nhau...
Bài 65 trang 167 SBT toán 9 tập 1
Giải bài 65 trang 167 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như trên hình 77...
Bài 64 trang 167 SBT toán 9 tập 1
Giải bài 64 trang 167 sách bài tập toán 9. Cho hình 76, trong đó hai đường tròn (O) và (O’) tiếp xúc nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau...