-
Vở thực hành Toán 8 - Tập 1
-
Vở thực hành Toán 8 - Tập 2
Giải bài 7 trang 124 vở thực hành Toán 8 tập 2
Với giá trị nào của m, đường thẳng y = mx + 1 (m ≠ 0)
Đề bài
Với giá trị nào của m, đường thẳng y = mx + 1 (m ≠ 0)
a) Song song với đường thẳng y = 3x?
b) Cắt trục hoành tại điểm có hoành độ bằng -2?
c) Đồng quy với các đường thẳng y = 5x − 2 và y = −x + 4 (tức là ba đường thẳng này cắt nhau tại một điểm)? Với giá trị m tìm được, hãy vẽ ba đường thẳng này trên cùng một hệ trục tọa độ để kiểm nghiệm kết quả.
Phương pháp giải - Xem chi tiết
a) b) Sử dụng tính chất hai đường thẳng cắt nhau, hai đường thẳng song song.
c) Phương trình hoành độ giao điểm của đường thẳng y = −x + 4 và y = 5x – 2.
Lời giải chi tiết
a) Đường thẳng y = mx + 1 song song với đường thẳng y = 3x khi hai đường thẳng có cùng hệ số góc, tức là m = 3.
b) Đường thẳng y = mx + 1 cắt trục hoành có hoành độ bằng -2, tức là nó đi qua điểm (-2; 0). Điều đó xảy ra khi m.(-2) + 1 = 0, tức là \(m = \frac{1}{2}\).
c)
- Trước hết tìm giao điểm của hai đường thẳng y = 5x – 2 và y = -x + 4. Vẽ hai đường thẳng ấy trên cùng một hệ tọa độ (HS tự vẽ):
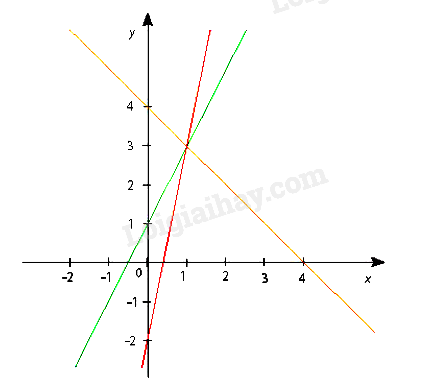
Trên hình vẽ ta thấy hai đường thẳng cắt nhau tại điểm (1; 3).
- Đường thẳng y = mx + 1 đi qua điểm (1; 3) nếu 3 = m + 1. Từ đó suy ra m = 2.
Vậy khi m = 2 thì ba đường thẳng đã cho đồng quy tại điểm (1; 3).
- Với m = 2, đồ thị của ba hàm số là ba đường thẳng như hình bên (HS tự vẽ).
Bình luận
Chia sẻ
- Giải bài 8 trang 125 vở thực hành Toán 8 tập 2
- Giải bài 9 trang 126 vở thực hành Toán 8 tập 2
- Giải bài 10 trang 126 vở thực hành Toán 8 tập 2
- Giải bài 11 trang 127 vở thực hành Toán 8 tập 2
- Giải bài 12 trang 128 vở thực hành Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
