-
Vở thực hành Toán 8 - Tập 1
-
Vở thực hành Toán 8 - Tập 2
Giải bài 11 trang 127 vở thực hành Toán 8 tập 2
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
Đề bài
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
a) ΔBIC $\backsim $ ΔEIF
b) $F{{B}^{2}}=FI.FC$
c) Cho biết AB = 6cm, BC = 3 cm. Tính EF
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí Thales đảo chứng minh EF // BC
b) Sử dụng các tỉ số đồng dạng của hai tam giác để chứng minh $F{{B}^{2}}=FI.FC$
c) Dựa vào định lí Thales cho EF // BC, ta có các tỉ số bằng nhau suy ra độ dài EF.
Lời giải chi tiết
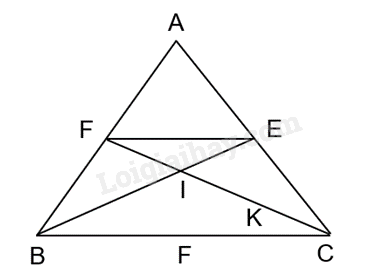
a) Do BE là đường phân giác của góc B nên $\widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}$, ta có: $\frac{EA}{EC}=\frac{BA}{BC}$ (1).
Tương tự với đường phân giác CF, ta có: $\frac{FA}{FB}=\frac{CA}{CB}$ (2).
Bởi vậy, từ (1) và (2) ta suy ra $\frac{EA}{EC}=\frac{FA}{FB}$, nghĩa là EF định ra trên hai cạnh AB và AC những đoạn thẳng tương ứng tỉ lệ. Do đó theo định lí Thales đảo ta có EF // BC. Từ đó suy ra $\Delta BIC\backsim \Delta EIF$ (đpcm).
b) Hai tam giác BFI và CFB có $\widehat{F}$ chung, $\widehat{{{B}_{1}}}=\frac{\widehat{ABC}}{2}=\frac{\widehat{ACB}}{2}=\widehat{{{C}_{2}}}$.
Do đó $\Delta BFI\backsim \Delta CFB\Rightarrow \frac{FB}{FC}=\frac{FI}{FB}\Rightarrow F{{B}^{2}}=FI.FC$ (đpcm).
c) Ta có EF // BC (chứng minh trên). Do đó: $\frac{BC}{EF}=\frac{AB}{AF}\Rightarrow \frac{BC}{EF}=\frac{\left( AF+FB \right)}{AF}=1+\frac{BC}{AB}=1+\frac{3}{6}=\frac{3}{2}$.
Từ đó suy ra EF = 3: $\frac{3}{2}$ = 2 (cm).
Bình luận
Chia sẻ
- Giải bài 12 trang 128 vở thực hành Toán 8 tập 2
- Giải bài 13 trang 128 vở thực hành Toán 8 tập 2
- Giải bài 14 trang 129 vở thực hành Toán 8 tập 2
- Giải bài 15 trang 130 vở thực hành Toán 8 tập 2
- Giải bài 10 trang 126 vở thực hành Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
